Schriften von Lutz Führer

Sehr geehrte Besucherin, sehr geehrter Besucher dieser Seite meiner Homepage!

Etwas weiter unten habe ich ein paar persönliche Meinungs-Beispiele und meine - vielleicht noch interessanteren - Schriften und Materialien nach diesen Sachgebieten jeweils chronologisch aufgelistet und - soweit rechtlich erlaubt - verlinkt (Einzelnes dabei auch in mehreren Rubriken):

- Fachwissenschaftliches - Fachmethodisches zum MU der Sek. II - Fachmethodisches zum MU der Sek. I
- Unterrichtsmethodisches zum MU der Sekundarstufen - Grundsätzliches zum MU und zur Lehrerausbildung
- Allgemein Mathematikdidaktisches - Geschichtliches zu Schulmathematik und Mathematikunterricht sowie
- Rezensionen

Zuvor möchte ich Ihnen allerdings ein paar Bemerkungen zu meiner seit 1975 gewachsenen Einstellung zur hochschulischen Lehrer/Innen/ausbildung anbieten. (Mit dem Link zu den Absätzen "Schriften und Materialen" können Sie das auch einfach überspringen.)

Vom schulpraktischen Sinn der Mathematikdidaktik:
Variieren - Kontextuieren - Relativieren
Interpretieren und Mitlernen Lehren!

Im Laufe eines recht langen Berufslebens ist meine Überzeugung gewachsen, dass der seelische, erzieherische und materielle Aufwand für "allgemeinbildenden" Pflichtunterricht in "Mathe für alle" dann und nur dann seine Kosten und Zwänge wert ist, wenn mit "dem Stoff" und all den unvermeidlichen Verhaltensrestriktionen für Lernende und Lehrende immer auch eigenverantwortlich sinngebendes Interpretieren - natürlich stets altersgerecht moderiert - vermittelt wird. Leider wird dieser zwischenmenschlich oft mühsamen und disziplinarisch heiklen Vermittlungsfunktion realen Unterrichts "oben" und "draußen" viel zu wenig Raum, Aufmerksamkeit und Anerkennung gewidmet. Dies gilt nach meiner Erfahrung sowohl für konstruktive Bemühungen der Schüler/Innen als auch für solche ihrer moderierend unterrichtenden Lehrkräfte und deren Besoldungen. "Guter Unterricht" im beschriebenen Sinne reicht allerdings selten für eine Lohnsteigerung aus, weil er gewöhnlich einer oder mehreren sehr förmlichen Beamten- oder Geschäftstrichtern bzw. -pyramiden untergeordnet ist.

Mathematisch Wahres, Richtiges oder auch nur korrekt Ermitteltes kann aber in zahllosen außermathematischen Gesellschaftsrealitäten nur selten "wirklich Wahres" bedeuten. Eine sehr alte Weisheit sagt: "Recht haben und Recht bekommen ist nicht dasselbe!" Für schmerzhafte Streitfälle "draußen", im alltäglichen Leben, gibt es seit Jahrtausenden gesellschaftlich "gehobene" Kasten und/oder priviligierte Institutionen, die teils gesetzlich ermächtigt, teils rituell tradiert, nicht selten auch esoterisch verklausulierend bestimmen dürfen - sei es auch nur kollegial akzeptiert - was im Einzelfall als recht oder Recht gelten soll, darf bzw. "muss"... (S.z.B. unten das trickreiche juristische Insiderwerkzeug >Substantiierung für Zivilprozesse< oder auch meine wegen ein paar Copyright-Hindernissen unveröff. Arbeit zur Entdeckungs-Geschichte incl. gesellschaftlicher Hintergründe des erst zweitausend Jahre später sog. Pythagoras-Satzes.)

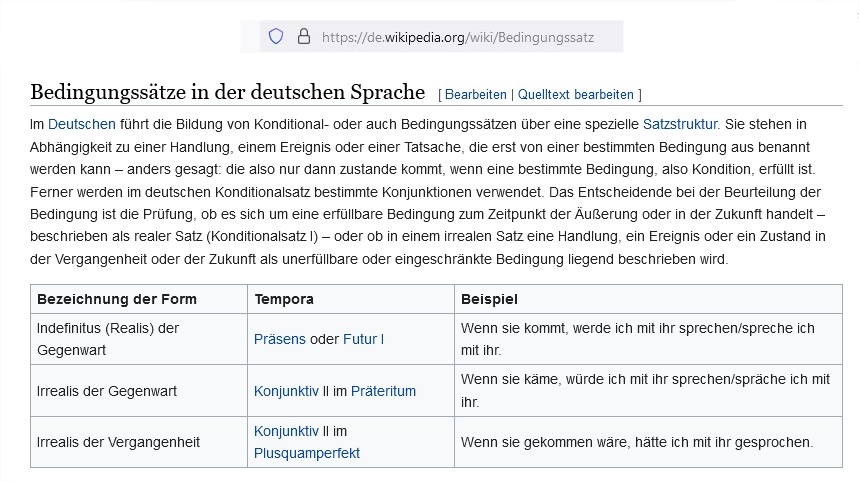
Die besonders sozialrelevante Aushandlungsbelastung der Lehrpraxis im Fach Mathematik wird im Schulsystem leider nicht nur traditionell, sondern inzwischen auch durch das politische und akademische Getöse zu - unvermeidlich auch banalisierenden - "internationalen Vergleichsstudien" wieder deutlich zunehmend abgewertet. Dabei ist mir leider auch bewusst, dass heute zwischenmenschlich existenzielle Relativierungen auch noch zunehmend quer zu den unaufhaltsamen Vormärschen "sozialer" Medien und Digitalisierungen eingeübt werden müss(t)en. Leider wird das auf den Displays der Smartphones immer schwieriger, denn Bedingungssätze passen dort kaum noch hinein (sowohl grafisch als auch kommunikativ):

(Diese Einsichten sind keineswegs neu: vgl. etwa den seit Elon Musks Erfolgen - wie etwa diese "Meldung von Anfang 2024" - mit dem inzwischen sehr gegenwartsnahen SF-Roman "Der Orchideenkäfig" von H.W. Franke, erschienen 1961, und die aktuell mit "ChatGPT" öffentlich explodierenden KI-Angebote (s.z.B. Bachelorarbeit in drei Tagen mit ChatGPT?; vgl. aber auch diesen aktuellen Überblick Ende März 2023 - von den viel älteren Klassikern von G. Orwells "1984" oder Huxley's "Brave New World" ganz zu schweigen... Als anregender Versuch einer vielseitigen Bestandsaufnahme mit Zukunftsperspektiven dazu könnte schon mal R. D. Prechts "Freiheit für alle" dienen, erschienen 2022...)

Nach dem Studium an der FU Berlin habe ich von 1968 bis 1975 an der TU Berlin in der wissenschaftlichen Mathematik gearbeitet. Während eines Forschungsaufenhaltes an der Universität Bonn 1972/73 wurde in der BRD das Kurssystem für die gymnasiale Oberstufe mit stark überzogenen wissenschaftstheoretischen und sozialen Erwartungen eingeführt. Aus anfänglicher Entrüstung (

1973, gem. mit H. Karcher) über diese Fehlentwicklung habe ich mich dann zunehmend mit Schulmathematik der Sekundarstufen und später auch mit entsprechenden Fragen des Mathematikunterrichts und der Mathematikdidaktik beschäftigt. Meine fachdidaktischen Schriften lassen sich entsprechend den Bereichen

Im Rückblick finde ich, dass Mathematikunterricht und Mathematikdidaktik seit TIMSS (ab dem letzten Jahrtausendende) und - gleich im Anschluss daran - den mit Tests und Schlagwörtern die westliche Schulwelt immer wieder kulturell egali- und trivialisierenden PISA-Abrechnungen allzu stark auf die Vermittlung zweifelsfrei abprüfbarer Fertigkeiten und Standardreflexe ausgerichtet werden. [Vielleicht ist das ja in den neueren OECD-Sudien 2021, 2022 bzw. 2023 samt ihren gleich mit angebotenen "Presse-Mitteilungen" neuerdings ganz anders. Vielleicht? Nach einigen früheren und aktuellen Pressezusammenfassungen habe habe ich sie mir erst einmal erspart.] Zu Vieles legt(e?) seit vielen Jahren solchen internationalen Vergleichstudien hauptsächlich Dressur- und Effizienzstatistiken statt Beobachtungen konstruktiver Entwürfe und Diskursversuche nahe. Folglich waren (sind?) die curricularen Rechtfertigungen dieser Ausrichtungen über ständische Dienst- und Vermarktbarkeit hinaus wohl eher wirtschaftspolitisch denn als konstruktiv sozial- oder allgemeinbildungsorientiert verständlich. (Vgl.z.B. den DMV-Leserbrief 1997 und den Text von H. Karcher 1998 sowie 2001, 2009a, dort pdf-S. 6 f. und 19 ff., mit 2009b oder auch 2012.)

Anders gesagt: Die rasant zunehmende, auf Drittmittel umgelenkte Zweckentfremdung der akademischen MaDi samt traditionell willfähriger Beihilfe zur Durchbürokratisierung und Dequalifizierung des öffentlichen Schulwesens einerseits und die Verwässerung des wissenschaftlichen Diskurses durch asoziale Kettenverträge mit entsprechenden Publikationshageln, Verlagskonzentrationen und Copyrightrestriktionen andererseits passen leider nur zu gut in dieses Bild. (Man vergleiche unsere zunehmenden sozialen Abspaltungen beim Corona-Home-Schooling nur einmal mit dieser Mahnung vom 24.08.2021 zum aktuellen US-amerikanischen Schulwesen: Returnung to 'Normal' in Education ....)

Wem allgemeinverbindlicher Mathematikunterricht und dessen akademische Didaktik noch in einer künftigen demokratischen, wenn auch weitgehend durchdigitalisierten Gesellschaft nützen, hängt - davon bin ich seit 1973 zunehmend überzeugt - entscheidend davon ab, inwieweit sich beide stets bei allen ihren "Kunden" um eine faire Balance zwischen allgemeinverbindlichem Strukturieren samt regelgerechtem "Auswerten" einerseits und dessen immer auch subjektivem Interpretieren andererseits bemühen. (Vgl. dazu etwa die Ausarbeitung 2009 des kritischen Vortrags aus 2007 "Was könnte zeitgemäßer Mathematikunterricht zu naturwissenschaftlicher Allgemeinbildung beitragen?", dort pdf-Seiten 1-3 und 171-192.)

Mathematisch Korrektes ist für die meisten Menschen nicht zwingend bzw. überzeugend und wohl auch solange belanglos, jedenfalls außerschulisch, wie es nicht "unmathematisch" kontextuiert ge- oder benutzt wird. Zahlen und auch Formeln sprechen nur in gewissen Kontexten für sich. Dies gilt insbesondere auch für vorgeblich "zwingende" statistische Datenüberblicke (vgl. z.B. meinen Essay "Misstrauensregeln" von 1997). Anders gesagt: "Für Draußen" - und auch das sollten allgemein-bildende Schulen lehren - stellen Mathematisierungen lediglich fair nachprüf- und kritisierbare Überschlagsrechnungen, Modelle und Strukturierungsmuster für komplexere Zusammenhänge und deren Be- und Auswertungen bereit... Außerfachlich wirklichkeitsrelevante Einsichten und Folgerungen beruhen in aller Regel unvermeidlich (auch) auf "außernathematischen" Interpetationen, also: allenfalls mathematisch gestützen ...

Was das für die Lehrpraxis im Mathematikunterricht nach meiner Überzeugung bedeuten sollte, habe ich im Abschnitt 7.3 meines Essays "Pädagogik des Mathematikunterrichts" 1997 (S. 127-129) auf ein paar Punkte und persönliche Fußnoten zu komprimieren versucht. Soll diese fachkritsche, pädagogisch und sozial motivierte Auffassung die traditionäll behavioristisch-autoritär überwöbte Schulpraxis im Schüler-, Bevölkerungs- und Gemeinschaftsinteresse pädagogisch leiten (können?), so müssen freilich die möglichen Erträge von Datenerhebungen und -auswertungen wie Klassenarbeiten, Pisa- oder Corona-Studien wie auch der Schulverwaltungsüberbau samt 1. und 2. Lehrer/Innen/ausbildungsphasen unterrichtspraktisch relativiert und immer wieder auch hinterfragt werden - was allerdings selten beförderungsschnittig wirkt - ...

Und leider sind gesellschaftspolitische Bemühungen um sozial emanzipierende Unterrichts- und Schulsystem-Reformen "von außen" in den vorigen Jahrhunderten unter durchaus wechselnden gesellschaftlichen Bedingungen immer wieder versandet.

1. Tempolimit

Warum - in Deutschland - keine flächendeckenden Tempolimits auf Autobahnen, Bundes- und Landstraßen eingeführt werden? Das ist doch wohl hinreichend bekannt: Man denke nur an unsere gehobene SUV-Industrie und ihre Lobbyist/In/en, an die Bequemlichkeiten im Innenraum, an das Image flotter Flitzer bei jüngeren Nachbarn, vielleicht auch an ein sehr mutiges FDP-Bekenntnis zur "Mobilitäts-Freiheit" mit diesem Gutachten im Hintergrund...

Dass man innerstädtische oder gar entferntere Ziele schneller erreicht, wenn man schneller fährt, dürfte freilich nichts als eine ignorante Illusion sein. Vgl. etwa die Aufgabe "Ein wenig schneller" (In: Mathematik lehren, Heft 11 - 1985, S. 14, s. auch im MUED-Arbeitsblatt von Oktober 2021) oder auch diese Einschätzung zum Zeit- und Geld-Sparen durch Tempolimits unter Bezug auf eine akuelle Studie des Umweltbundesamtes ...

2. Corona

"Die bundesweite Sieben-Tage-Inzidenz steigt laut RKI leicht auf 316,0 von 315,6 am Vortag.
Die Sieben-Tage-Inzidenz gibt die Sieben-Tage-Anzahl der Neuinfektionen innerhalb einer
Woche je 100.000 Einwohner an."
(ARD-Text, S. 107, 2. Abs., am 20.12.2021, 20.00 Uhr.)

Was soll das den einzelnen Bürger/Inne/n angesichts einer eher unübersichtlichen als repräsentativen
Erhebungspraxis, zudem mit einer belanglosen Nachkommastelle, eigentlich belegen oder auch nur
suggerieren - außer dass ein 7-fach aufgebauschtes statt täglich gemitteltes Infektionsrisiko seit den
Vortagen mal mehr oder minder rasch gestiegen oder gesunken ist? Warum wurde nicht von vornherein
mit vergleichbaren Erkrankungs- und Sterberaten früherer Jahre bzw. Epidemien argumentiert? Wären
unsere Normalbürger/Innen mit (gerundeten) lokalen, regionalen oder landesweiten Erhebungsquoten

Infizierte : (repräsentativ wofür?) Getestete

überfordert gewesen und hätten dann einfach alles trivialisiert? Wozu dann Mathematik-Pflicht für alle???

Immerhin: In der 20 Uhr-Tagesschau der ARD hörte ich am 4. Juni 2022 immerhin nach dem Aufsagen der aktuellen 7-Tage-Corona-Inzidenz erstmals: "Allerdings ist zu berücksichtigen ... und dass nur positiv Getestete in die Statistik einfließen." Und am 20. Juni 2022 verkündet der Spiegel ganz spontan, dass "montags der Inzidenz nicht mehr zu trauen" sei... Der Spiegel verzichte daher künftig sonntags und montags darauf, "den [7-Tage-Inzidenz-Wochenend-] Wert aufzugreifen". (s. Link).

Ob sich die durchgreifenden Corona-Schutzmaßnahmen (ab März 2020) als präventiv angemessen, epidemiologisch erfolgreich oder gar gesellschaftlich ermutigend erweisen werden, kann ich nicht wirklich einschätzen - das auch angesichts absehbarer, immer noch sehr unübersichtlicher individueller Begleit- und Folgeschäden wie auch wirtschaftlicher Umstrukturierungen und in deren Folge dann wohl auch nachhaltiger - z.T. weltweiter - humaner, gesellschaftlicher und ökologischer Katastrophen samt "Wanderungs"bewegungen.

Was mich ab Frühjahr 2020, im Rückblick auf mein Berufsleben als Mathematiklehrer und Lehrerausbilder, traurig machte, waren die andauernd plakativen Scheinbegründungen aus Politik und Massenmedien für flächendeckende Präventivmaßnahmen und -regeln, die sich ohne Rücksicht auf etwaige Verzerrungen immer wieder auf (absolute) Einzelfallsummen statt auf Quoten zu klar umrissenen Zufallsstichproben beriefen, z. B. auf klar definierte oder glaubhaft repräsentative Stichprobenauswahlen, auf Wiederholungsanteile Infizierter oder auch Berichte aus PCR- oder Schnelltests an (scheinbar?) un-/symptomatischen Menschen, an Verdachtsfällen, an tatsächlichen Corona-Symptomatischen und/oder halbwegs unterschiedlichen Todesfolgen eindeutig aufgrund, mit oder ohne Corona-Begleitinfektion.

Wie kann es sein, daß sich das RKI noch im Oktober 2021 mithilfe "neuer Stichproben-Auswertungen" die pausenlos beklagten deutschen Impfquoten mal eben neu auf 10% mehr schätzt oder medizinische Spezialisten immer noch um Bezug auf repräsentative statt beliebiger Stichproben bitten? (Vgl. hierzu etwa diesen erschütternden Rückblick im "Corona nachgefragt" - Interview mit Prof. Streeck vom 08.Oktober 2021 oder auch das höchst aktuelle Interview mit ihm vom 15. Dez. 2021 auf Servus-TV. Noch deutlicher findet sich die Kritik zur Corona-Stichproben-Manipulation als "Ein Nachdenkzettel [Sommer 2022]" in der Neuauflage von Alfred Schreibers "Die enttäuschte Erkenntnis - Paramathematische Denkzettel", Logos-Verlag, S. 27-31.)

Am Ende der Mittelstufen sollten eigentlich möglichst viele Schüler/Innen, egal welchen Schultyps, (auch) gelernt haben: Statistische Schlüsse aus nicht-repräsentativen, verdächtig situativ und international kaum vergleichbar erhobenen Stichproben mit z.T. undurchsichtig variablen Bezugspopulationen sind naturgemäß zweifelhaft. (Vgl. etwa meine Texte zu Misstrauensregeln, zur Fehlerkunde oder auch die Glosse zu Mittelwerten.) Aus statistischer Sicht taugten folglich die seit März instrumentalisierten Erhebungsdaten nicht als hinreichende Begründung für die massiven staatlichen Vorsichtsmaßnahmen. (Vgl. etwa das Spiegel-Interview von Ende März 2020, diese kritischen Interviews vom 29. April bzw. 09. Sept. 2020 mit S. Bhakdi auf Servus-TV bzw. das fachkritische Buch Corona Fehlalarm? oder auch das SZ-Video von H. Elbert und C. Jocher-Wiltschka vom August 2020 oder auch den aktuellen Aufsatz von H.-J. Bandelt und das SZ-Video vom 05.07.21 zu anhaltend undurchsichtigen Teststrategien.)

Immerhin: Ersatzweise wurde täglich suggeriert, die Johns-Hopkins-Universität, das RKI und viele prominente Virologen hätten einen so bedeusamen Ruf, dass man ihren Ergebnissen und den politischen Entscheidungsträgern vertrauen sollte, dabei Vergleichsdaten aus früheren oder auch aktuellen Grippewellen getrost ignorieren dürfe und ihnen leider, leider auch individuelle wie soziale Begleitschäden aus Zeitnot unterordnen müsse... Und: Die in Deutschland und weltweit beschlossenen restriktiven Vorsichtsmaßnahmen auf der Basis von ( vor-/gestrigen?) PCR-Testwerten, unklaren Sterberaten, schwankenden Übersterblichkeiten und Krankenhausreserven wirkten offensichtlich in Öffentlichkeit und Politik erfreulich rascher, überzeugender und entlastender als unbequem vielschichtig, evtl. auch kontrovers, abwägende Begründungen der politisch eigentlich verantwortlichen Entscheidungsträger, incl. der doch wohl dafür (auch) gewählten Parlamente. (S. z. B. diese TV-Diskussion vom 21.10.2020 oder auch Google zum Thema "Schäden durch Corona-Maßnahmen").

3. "Ausländer"statistik"

Vorurteile mit Hilfe nicht repräsentativer Kriminalstatistik schüren: Dazu empfehle ich dieses lehrreiche SZ-Video von Herrn Ronen Steinke zur "Ausländer"kriminalität als Stundeneinstieg. (Falls nicht mehr zugänglich, tut es auch sein Text von 2019.)

4. Statistische "Überblicke"

Statistische Überblicke liefern eher Fragen als Antworten, s. etwa die jeweils aktuellen Infos zur Sonntagsfrage. Und dieses Video zur Sozialen Ungleichheit "Wer hat, der kriegt" könnte Schüler/Innen einmal zu kontroverser Gruppenarbeit anregen... (Weitere ernsthafte Überblicke finden sich z.B. auch in diesem amtlichen Datenreport.)

5. Brüche, "Quoten" oder numerisch aufgeblähte "Inzidenzen" statt Verhältnismäßigkeiten?

Die öffentlichen Corona-Anordnungen erinnern mich leider täglich an die fachdidaktische Vernachlässigung des Verhältnisbegriffs hinter der besser testbaren Bruchrechnung; s.z.B. mein Vortragsmanuskript von 1998/99 bzw. dessen Überarbeitung 2003.

Die Beispiele zeigen nicht zuletzt, dass die testschnittige Betonung der Bruchrechnung in der Orientierungsstufe leider zu einer Marginalisierung der Verhältnisbegriffe als "Zahlenpaare" und damit ihrer stets auch subjektiven Interpretationen als "Größenwerte" geführt hat. (Vgl. etwa das Vortragsmanuskript von 1998, die didaktische Themenfeldskizze in "Design Science" 1999, S. 82 f., oder auch die Ausarbeitungen von 2003 und 2007, S. 791-794.) So entsprachen und entsprechen die öffenlichen Mitteilungen der Tagespresse über Äußerungen und Entscheidungsgründe der deutschen Entscheidungsträger/Innen während Corona-Krise/n und angesichts krimineller Ausfälle im Allgemeinen nicht dem, was mathematische Grundbildung (möglichst) allen heranwachsenden Bürger/Inn/en mit den beiden heute wohl wichtigsten Grundpfeilern Näherungsrechnen und Statistical Literacy anerziehen sollte: demokratisch fundiertes, aufgeklärtes und handlungsbereites Mitdenken, wenn es um Maß, Zahl oder funktionale Abhängigkeiten geht. Außerhalb der Schulen spielen mathematisch exakte Zusammenhänge bei menschlichen Entscheidungen nur selten die Hauptrolle. (Nachdenkliches dazu s. diese aktuellen Beispiele: Tipp 1 oder auch Tipp 2.) Anders gesagt: Zahlen sprechen (fast) nie für sich selbst! Wo sonst sollten möglichst alle mitverantwortlichen Bürger/Innen einer Demokratie "wissenschaftlich belegtem" Argumentieren mit statistischen Daten aus vage umschriebenen Stichproben erst misstrauen und dann überzeugt(er) trauen lernen, wenn nicht im Mathematikunterricht?

6. Ob und was mathematische Ergebnisse "draußen" bedeuten besagen dort erst zwischenmenschliche Kontextuierungen...

Dazu sollte auch gehören, die förmlichen, formallogischen, absichtlich unpersönlichen Beweisansprüche der Mathematik immer wieder einmal an den gesellschaftlich übergeordneten, in aller Regel eher vage formulierten und nicht selten verführerisch verklausulierten "Bürgerlichen" Gesetzesregeln zu reflektieren. Dazu vgl. etwa zur BGB-Praxis das juristische Zauberwort Substantiierung oder - sozusagen als Eingangstor in die höhere Schulmathematik - diese wg. Copyright-Hindernissen unveröff. Arbeit zum epistemologischen Hindergrund des viel später sog. Pythagoras-Satzes.

7. Mathematische "Grundbildung" für alle?

Im einstmals klassischen "Handbuch für den Mathematikunterricht an Grundschulen" von Hendrik Radatz und Wilhelm Schipper aus 1983 (sinngemäß zit.n. 4. Aufl. 2004, S. 20) fand ich einige sehr treffende Wertungen, die ich im heutigen, von digitalen Medien bedrängten Mathematik-Pflichtunterricht an allgemeinbildenden Schulen, durchaus nicht nur an Grundschulen, und in seiner eigentlich prosperierenden Hochschuldidaktik schmerzlich vermisse:

"Es gibt vielleicht keine weltanschauliche Mathematik, wohl aber eine gesellschaftlich geprägte
Erziehung und somit auch einen in den Zielen und Inhalten unterschiedlichen Mathematikun-
terricht. Die Ziele des Mathematikunterrichts sind auch abhängig von dem, der sie formuliert."
(Sei es bewusst oder - und viel öfter - : unbewusst. L.F.)

... "Der Mathematikunterricht der Grundschule kann nicht so einfach wie vor Jahrzehnten als alleinige und zentrale Aufgabe anstreben, möglichst gute Rechner auszubilden und in die Sekundarstufe I zu entlassen. Die Anforderungen, Qualifikationen und Erwartungen der Umwelt sind sehr viel größer und komplexer geworden." (Und werden dabei leider zunehmend noch von Schnellschüssen aus Turbo-Meinungsmedien unterwandert. L.F.)

Danach heißt es mit einer Anleihe aus J. Diederich's behutsamer Freudenthal-Kritik "Vom Fluch der Liebe zur Mathematik" (aus JMD 1, 1980, S. 277-207):

"Für Nichtmathematiker spielt die allgemeine Bildung [lehrerseits - auch beim Mathematik-Unterrichten, L.F.], die Grundanforderungen an die Schüler [,] eine wesentlichere Rolle als die fachliche Bildung, fühlen sie sich darüber hinaus doch eher den Schülern verpflichtet, die Mathematik nicht lieben oder wählen, sondern als Pflichtfach in der täglichen Unterrichtspraxis erdulden müssen.

So beschreibt etwa Diederich (1980) als Bildungsziel des mathematischen Unterrichts, den volkstümlichen Glauben an die Mathematik zu erschüttern, damit jeder vernünftige Mensch beurteilen kann, was man Mathematikern anvertrauen kann und was nicht. Eine vergleichbare Zielformulierung hatte [hätte eigentlich?, L.F.] auch Gültigkeit für alle hochspezialisierten Berufsgruppen, wie z. B. Mediziner, Psychologen, Bildungsplaner ...

Der Mathematikunterricht [nicht nur] der Grundschule kann nicht so einfach wie vor Jahrzehnten als alleinige und zentrale Aufgabe anstreben, möglichst gute [Be-] Rechner auszubilden und in die Sekundarstufe I zu entlassen. Die [zukünftigen! L.F.] Anforderungen, Qualifikationen und Erwartungen der Umwelt sind sehr viel größer und komplexer geworden."

... Und der öffentliche Meinungsaustausch ist im scharfen Gegensatz dazu plakativer, nicht selten auch rabiater geworden! Möchte ich, L.F., heute, Ende 2021, ergänzen...

Miteinanderreden und begründetes Urteilen aller Schüler/Innen sollten im Mathematikunterricht eine besondere Rolle spielen, weil Mathematisieren, durchdidagitalisierter Unterricht und "Soziale" Medien allzu leicht zum tadellosen Funktionieren und Aburteilen drängen. Emanzipatorische und zugleich soziale Bedeutungen allgemeinverbindlicher Mathematik können meist nur über zwischenmenschlichen Umgang mit Mathematischem vermittelt und/oder ausgehandelt werden. Sie sind korrekter Mathematik m. E.s nicht immanent. Lehrer/Innen sollten auch nicht - und sei es aus disziplinarischen oder testschnittigen Gründen - so tun, als wären sie es. Meine didaktischen Bemühungen galten deshalb immer wieder auch einem Mathematikunterricht als Schule des Selber- und Mitdenkens über das Mathematiktreiben und -benutzen. Also, gehobener augedrückt: einem allgemeinbildenden, enkulturierenden und sozialisierenden Mathematik-Unterricht, der einer gemeinschaftlichen, insbesondere nicht ständischen, dafür aber empathischen, demokratisch fairen und toleranten Erziehung zuarbeiten sollte. Und nicht zuvörderst behavioristischen Dressuren und Erfolgsmessungen an lernenden, lehrenden oder forschenden Menschen - von naivem Wissenschaftsglauben ganz zu schweigen. (Vgl. etwa diesen Überblicksversuch zu math.-naturw. Allgemeinbildung in 2009a, dort pdf-S. 6 f. und 19 ff., sowie 2012.)

1971	Theorie des Abbildungsgrades in endlich-dimensionalen Räumen. Dissertation (unveröffentlicht). Berlin: Freie Universität.
^'1972	Ein elementarer analytischer Beweis zur Eindeutigkeit des Abbildungsgrades im Rⁿ. In: Mathematische Nachrichten, Band 54 (1972), S. 259-267 (Link). Schwerpunkt: Hauptergebnis der Dissertation. Vgl. etwa Nussbaum (S. 635 oben), Amann/Weiss (S. 1 unten), Benevieri/Furi (S. 2) oder Outelero/Ruiz (insbes. S. 1 und S. 38 f.).
1977	Allgemeine Topologie mit Anwendungen. Braunschweig/Wiesbaden: Vieweg. Schwerpunkt: Verschmelzung struktureller und analytisch-anwendungsorientierter Zugänge, insbes. aus der Analysis und Funktionalanalysis.

*Fachmethodisches zum MU der Sek. II*
1973	Wie man Mathematik nicht unterrichten sollte. Vervielf. Manuskript, Universität Bonn. (Gem. mit H. Karcher.) Manuskript Schwerpunkt: Aufforderung, die damals sehr hochtrabenden nordrhein-westfälischen Kursvorgaben zur „neugestalteten gymnasialen Oberstufe“ auf mathematische Grundbildung zu säkularisieren. (Teilweise in die Denkschrift der DMV zum Gymnasialunterricht 1976 eingeflossen.)
1979	Objektstudien in der Vektorgeometrie. In: Didaktik der Mathematik 7.1, S. 32-61. Link (Text mit kurzem Nachtrag 2015) Schwerpunkt: Vorschläge, Kurse in Linearer Algebra und/oder Ananlytischer Geometrie aus geometrischen Objekten im R³ zu entwickeln.
1981	Zum Gehalt der elementaren Integralrechnung in ideengeschichtlicher Sicht. In: Der Mathematikunterricht 27.5, S. 7-60. Schwerpunkt: Wandlungen der schulrelevanten Integralbegriffe.
1982	Die Kreisberechnung als Brennspiegel der Schulmathematik, 2 Teile. In: Praxis der Mathematik 23.10, S. 289-298 und Praxis der Mathematik 23.11, S. 323-337. Schwerpunkt: Teil 1 (s. unten: Sek. I); Teil 2 (Sek. II): Ableitung von Sinus und Kosinus ohne Grenzwerte und Additionstheoreme, nützliche Ungleichungen, berühmte Kreisberechnungen, lineare und quadratische Konvergenz.
1982	Analysis für alle? Begründungen, Ziele und Schwerpunkte im Pflichtbereich. In: Bericht über die 8. Tagung der Fachleiter für Mathematik, Schriften der MNU, Heft 30, S. 24-31. Text + Anlagen Schwerpunkt: Rechtfertigungen und sinnvolle Schwerpunkte des pflichmäßigen Analysisunterrichts. (Vgl. dazu die neuere Arbeit, S. 103-136 in Link.)
1982	Analysis als Pflicht? – Begründungsversuche, Trends und Neuansätze. In: Fragen der Differenzierung im Mathematikunterricht der gymnasialen Oberstufe (Hrsg.: H. Pfeiffer, H.-G. Steiner). Bielefeld: IDM, S. 143-154. Link Schwerpunkt: Rechtfertigungen und sinnvolle Schwerpunkte des pflichmäßigen Analysisunterrichts.
1983	Was trägt die „zweite Säule“? – Lineare Algebra und Analytische Geometrie auf der Sekundarstufe II. In: Bericht aus dem Seminar für Didaktik der Mathematik, Univ. Bielefeld, S. 29-33. Link Schwerpunkt: Rechtfertigungen und sinnvolle Schwerpunkte des pflichmäßigen Unterrichts in Linearer Algebra und/oder Analytischer Geometrie.
1983	Stellungnahme zu den „Einheitlichen Prüfungsanforderungen in der Abiturprüfung“ („EPAs-Beschluss der KMK“ von 1979). In: Praxis der Mathematik 25, S. 117-119. Link Schwerpunkt: Protest gegen die Standardisierung von Prüfungsaufgaben. (Mit anschl. Widerrede von Wolfgang Kroll.)
1984	Mittelwert - Mittelmaß - Mittel zum Zweck? In: Mathematik lehren, Heft 3, S. 1. (s. Link) Schwerpunkt: Glosse zu Verzerrungen durch irreführend glättende Mittelwertbildungen und Durchschnittsvergleiche mit normativen Auswirkungen. (Vgl. unten die Aufsätze zu "Misstrauensregeln" von 1997 bzw. zu verschiedenen Mittelpunkt-Begriffen für Vierecke von 1985.)
1985	Sehr hohe Genauigkeiten. In: Mathematik lehren, Heft 13, S. 62-67. Schwerpunkt: Wozu werden sehr hohe Genauigkeiten ernsthaft gebraucht?
1989	Fünf Wege zur Parabelfläche. In: Mathematik lehren, Heft 37, S. 35-39. Hinweis: Eine weitere elementarte Herleitung der Parabelfläche findet sich am Ende des Aufsatzes „ Heuristik und Geschichte der elementaren Volumenberechnung“ von 2006; vgl. auch den Aufsatz von 1981 zur Geschichte der elementaren Integralrechnung (s. o.).
1996	Ellipsen, Exzenter und Epizykel – Die Genesis der geometrischen Astronomie als Vorgeschichte der Mathematik. (Manuskript, 69 S.) Link Schwerpunkt: Quellen, Grundideen und einfache Zugänge zum ptolemäischen Weltmodell. Hinweis: Manitius' klassische und gut lesbare deutsche Übersetzung des Almagest ist übrigens inzwischen online verfügbar: Band 1 bzw. Band 2.
1997	Mißtrauensregeln im Stochastikunterricht der Sek. II. In: Mathematik lehren, Heft 85, S. 61-64. Schwerpunkt: Daten, Schaubilder und statistische Maßzahlen sprechen nie für sich. Deshalb empfiehlt sich mancherlei Misstrauen bei der Interpetation von Stichproben- und auch Vollerhebungen... S. a. Manuskript 1997.
1998	Falsche Ansätze? – Geschicktes Probieren! ( Kurzfassung; Manuskript sowie gekürzt als „Geschicktes Probieren“ in: Mathematik lehren, Heft 91, S. 50-54.) Schwerpunkt: Vom Falschen Ansatz zur Differentialrechnung – Probieren als Fundamentale Idee; informelle Einführung der Regula falsi.
2004	Die Skisprungszene – Unnötige Belastungen für die Springer? (Gemeinsam mit H. Böer.) In: Mathematik lehren, Heft 125, S. 58-62. Schwerpunkt: Bei der Modellierung der Kontur der Willinger Sprungschanze mit Hilfe einfacher Newton-Interpolationskurven, Modellanpassung, Fehleranalyse und Interpretationsvorschlaegen wird deutlich, wie man aus Fehlern dazulernen kann. Mittel der Wahl: eine gestückelte Interpolationskurve und die Rolle der Ableitungen an ihren Nahtstellen.
2005	Geniale Ideen und ein lehrreicher Fehler des berühmten Herrn Galilei. In: Mathematica didactica 28.1, S. 58-78. Schwerpunkt: Es geht um lehrreiche Hindernisse bei der Entdeckung der Brachistochrone.
2009	Verstehen oder Berechnen?? - Wie passt der Computer zum Analysisunterricht des 20. Jahrhunderts? In: "Tagungsbericht 2008/09" des AK MUI, erschienen im Franzbecker-Verlag, 2012, S. 103-136. Der Text ist online verfügbar unter Link. Hier ist der Vortrags-Foliensatz. Schwerpunkt: Entwicklung derAnalysisdidaktik im 20. Jh.; instituetische und bildungspolitische innere Widersprüche; aktuelle Begründungsnöte; Plädoyer für Datenmodellierung als durchgängige Leitidee für beide Sekundarstufen. (Zu Siegfried Bernfelds Begriff "Instituetik" aus seinem Sisyphus-Buch (dort Buch-Seite 22 f.), der sich durchaus nicht nur auf Kindergarten-Pädagogik bezieht, vgl. den Anhang meiner Antrittsvorlesung von 1994 sowie einführend z. B. den Vortrag von Achim Leschinsky, dort insbes. S. 11 u., f.)

*Fachmethodisches zum MU der Sek. I*
1977 1978	Zur Methodik des Mittelstufenunterrichts, 2 Teile. In: Didaktik der Mathematik 5.4, S. 251-273, bzw. in: Didaktik der Mathematik 6.1, S. 26-53. Schwerpunkte: Unterrichtsbeispiele zur stärkeren Vernetzung der traditionellen Teilgebiete Geometrie, Algebra und Stochastik. In Teil 1 (Klasse 7-8): Einstiege zur Geom., Rechnen mit rationalen Zahlen, Ortslinien, Funktionen, Raumgeometrie. - In Teil 2 (Klasse 9-10): Strahlensätze, Einführung von Irrationalzahlen, Pythagoras-Satzgruppe, quadratische Funktionen und ihre Nullstellen, ganzrationlae Funktionen, Exponentialfunktionen und Logarithmen, trigonometrische Funktionen.
1982	Didaktik minus Stoff gleich Methodik? In: mathematiklehrer, Heft 1, S. 27-29. Link Schwerpunkt: Geometrie von der Wirklichkeit her, nicht von Strukturen oder „Grundlagen“!
1982	Die Kreisberechnung als Brennspiegel der Schulmathematik, 2 Teile. In: Praxis der Mathematik 23.10, S. 289-298, und Praxis der Mathematik 23.11, S. 323-337. Schwerpunkte: In Teil 1 (Sek. I): Kreisgleichungen, Bogenhalbierung mit ebenen Vektoren, Berechnung des Kreisumfangs, Definition und Berechnung der Winkelfunktionen, Kreisbewegungen, Additionstheoreme, Überlagungerung von Schwingungen, komplexe Zahlen. - Zu Teil 2 (Sek. II-Themen) s. o.
1983	Geometrie aus der Tiefe - Eine Einführung in die Geometrie auf dem Boden niedersächsischer Tatsachen (Sek. I) (Haupttext ; Zusätze) Schwerpunkt: Schwerpunktsetzungen, Begründung und Beschreibung des Geometrieunterrichts in einer 7. Klasse (ohne Geometrie-Vorkenntnisse aus der - seinerzeit schulformunabhängigen - Orientierungsstufe).
1984	Der Punkt von Fermat und Torricelli. In: Mathematik lehren, Heft 7, S. 54-56. Schwerpunkte: Computerexperimente zum Erraten der Lage des Punktes mit der kleinsten Abstandssumme zu den Ecken eines Dreiecks; Motivation des Begründens (BASIC-Programm).
1985 2005	Welche Vierecke haben einen „Mittelpunkt“? In: Mathematik lehren, Heft 8, S. 38-47. (Wiederabdruck in Weigand, H.-G.: ml-Sammelband Geometrie. Velber: Friedrich/Klett 2005, S. 18-27.) Schwerpunkte: Mittelpunkt“ in verschiedenen Konnotationen – Begriffsfeldentwicklung (parallel zu statistischen Mittelwerten).
1985	Ein wenig schneller. In: Mathematik lehren, Heft 11, S. 14. Schwerpunkt: Ein Beispiel für funktionales Denken in Klasse 7/8.
1985	Rotation. In: Mathematik lehren 11 (1985), S. 15. Beispiel: Welcher Körper entsteht, wenn man die Fläche zwischen einem symmetrischen Parabelbogen und der "x-Achse" erst um letztere und dann um die Symmetrieachse des Bogens dreht? (Zwanglose Einführung von Raumkoordinaten.)
1985	Annjewandte Mathematik. In: Mathematik lehren 11, S. 15. Beispiel: Kleine Episode zum Thema: Die Kreisberechnung verstehen heißt noch lange nicht, sie nutzen können.
1985	Rechner im Mathematikunterricht – Einleitung zum ml-Heft „Rechner II“. In: Mathematik lehren, Heft 13, S. 2-3. Schwerpunkt: Zeitgenössischer Stand und künftige Perspektiven des Rechnereinsatzes für den MU.
1985	„BASICs“. In: Mathematik lehren, Heft 13, S. 24-38. Schwerpunkt: Einführung für Neuntklässler ins Programmieren im Rahmen des MU an mathematisch oder informatisch wesentlichen Problemkreisen.
1996 2001	Kubische Gleichungen und die widerwillige Entdeckung der komplexen Zahlen. ( Manuskript von 1996) Gekürzte Fassung erschienen in: Praxis der Mathematik 43.2, S. 57-67. Schwerpunkte: Die Entdeckung der komplexen Zahlen gilt als Abfallprodukt der cardanischen Formel zur Auflösung der kubischen Gleichung. Der Aufsatz versucht deren Entdeckungsweg elementargeometrisch zu rekonstruieren. Anschließend wird die weitere Entwicklung bis zu den ersten Nichtexistenzsätzen im frühen 19. Jh. skizziert, die zur Geburt und Sichtweise der „modernen“ Algebra führten. - Insgesamt ergeben sich zwei Beispiele zur historisch-genetischen Methode.
1997	Zur frühen Feldmessung. In: Mathematica didactica 20.1, S. 20-25. Schwerpunkt: In alten Kulturen wurden viereckige Felderflächen wie Rechtecke mit den Seiten berechnet, die sich als Mittelwerte von Gegenseiten ergaben. Wie gut ist das?
1998	Falsche Ansätze - Probieren als fundamentale Idee. In: Beiträge zum Mathematikunterricht, S. 196-199. Schwerpunkte: Einfacher und doppelter Falscher Ansatz; Regula falsi.(Siehe dazu auch.)
1998	Logos und Proportion - Gestaltliche Aspekte von Bruchzahlbegriff und Bruchrechnung. (Ausgearb. Vortragsmanuskript Köln, 30. Juni 1998.) Schwerpunkt: Theoretische Hintergrundstudien zu „Verhältnisse – Plädoyer für eine Renaissance des Proportionsdenkens“, s. u. 1999 (Brüche bzw. S. 82 f. in "Design Science"), 2004 (Verhältnisse) und Dreisatz.
1999	Brüche - Lebensnähe - Bruchrechnung. In: Beiträge zum Mathematikunterricht. Hildesheim: Franzbecker 1999, S. 185-188. Schwerpunkte: Typische Probleme, Aspekte des Bruchzahlbegriffs, insbesondere Rechenzahl- und Verhältnisaspekt.
2001	Fachwissenschaftliche Grenzen und stoffdidaktische Probleme der elementaren Stereometrie (Vortrag auf der GDM-Jahrestagung). Online unter: Link. Schwerpunkte: Begriffliche, inhaltliche und strukturelle Probleme der Raumgeometrie für die Schule (u. a. Satz von Dehn). (Theoretische Vorstudien zur Arbeit von 2006 über "Siehe"-Beweise, s. u.)
2004	Verhältnisse - Plädoyer für eine Renaissance des Proportionsdenkens. In: Mathematik lehren, Heft 123, S. 46-51. Schwerpunkt: Verhältnisse und Proportionen berücksichtigen viel stärker als Brüche gestaltliche, bewertende und anwendungsrelevante Kontexte. Sie sind die Schlüssel zur Mathematisierung und Problematisierung von Dreisatzkonstellationen (Proportionalität?), und sie sind strukturell anders als Brüche. (Themenskizze dazu s.S.82 f. in "Design Science"; längere Manuskripte mit Vorstudien dazu aus 1999 bzw. "Proportionen" aus 2003.)
2004	Der Preis eines Kredits oder Wie man mit legalen Denkfehlern Kunden verleitet. In: Mathematik lehren, Heft 125, S. 20. Schwerpunkt: Nominal- versus Effektivzins.
2006	„Siehe“-Beweise für elementare Volumenbestimmungen. In: Beiträge zum MU, S. 203-206. (Kurzfassung des nächsten Aufsatzes.) Online unter: Link. Schwerpunkt: Welche Typen von Raumkörpern können im Rahmen der Sek. I sinnvoll beschrieben und berechnet werden, auch als Vorbereitung der Sek. II-Geometrie? Als besonders fruchtbar haben sich dafür – auch historisch – Ähnlichkeitsbetrachtungen und verallgemeinerte Scherungen (Cavalieri-Prinzip) erwiesen.
2006	Heuristik und Geschichte der elementaren Volumenberechnung. In: Mathematica didactica 29.1, S. 69-101. Online unter: Link. Schwerpunkte: Welche Typen von Raumkörpern können im Rahmen des MU der Sek. I sinnvoll so beschrieben und berechnet werden, dass nebenbei auch Sek. II-Geometrie vorbereitet wird? Als heuristisch besonders fruchtbar haben sich dafür – auch historisch – Ähnlichkeitsbetrachtungen und das Cavalieri-Prinzip (verallgemeinerte Scherungen) erwiesen. Wenn die Versicherung der Lehrerin oder des Lehrers atmosphärisch ausreicht, dass das Cavalieri-Prinzip für die behandelten Körper in der Sek. I garantiert problemlos sei, kann durchaus auch an Schwierigkeiten (Paradoxien) der schichtenweisen Dimensionsreduktion herangeführt und so ein Motiv für den späteren Definitionsaufwand mit dem Integralbegriff bereitgestellt werden. (Vgl. die Vorstudien dazu von 2001; s. o.)
2007	„Dreisatz“ oder Wieviel Volksbildung darf’s denn sein? In: Beiträge zum Mathematikunterricht 2007, S: 791-794. Online unter: Dreisatz. Schwerpunkt: Unterrichtsstandards für die vernetzten Themenkreise Dreisatz – Proportionen – lineare Funktionen haben zu verschiedenen Zeiten unterschiedlichen Auffassungen von Volksbildung entsprochen. (Vgl. die Arbeiten von 1998 (Proportionen), 1999 (Brüche) und 2004 (Verhältnisse).)
2009	Vom Begründensollen zum Vermutenwollen. In: M. Ludwig, R. Oldenburg, J. Roth (Hrsg.): Argumentieren, Beweisen und Standards im Geometrieunterricht. AK Geometrie 2007/08. Hildesheim: Franzbecker 2009, S. 167-188. (Online unter: Link; dort pdf-Seiten 171-192. - Vgl. auch das Manuskript von 2008 Geometrieunterricht abstrakt....) Schwerpunkt: Ziel des allgemeinen Unterrichts auf den Sekundarstufen kann wegen ihrer zunehmenden Einschmelzung ("Enttypisierung"), Bürokratisierung und inneren Diversifizierung nicht mehr das Beweisenlernen sein. Der an sich wünschenswerten Verbreiterung und Demokratisierung der Bildungsbeteiligung könnte mehr Bescheidenheit durch Konzentration auf eine Erziehung zum Vermuten- und Argumentierenwollen besser entsprechen.
2009	Archi's Trick? ( kurze ppt-Datei ; lange ppt-Datei ; lange pdf-Datei) Schwerpunkt: Wie Archimedes vielleicht auf seine Idee der Winkeldreiteilung gekommen sein könnte...
2011	Wege zum Pythagoras-Satz. (Manuskript. - Lange Ausarbeitung nach einem Vortrag vom 24. Sept. 2011 im AK MUI.) Schwerpunkt: Welche Zugänge zum Satz des Pythagoras sind im Laufe der letzten hundert Jahre vorgeschlagen worden, und wie sind diese Vorschläge didaktisch zu bewerten? (Vgl. auch unten, 2014 zu YBC7289.) Recherche zu folgendem Problem: Der sog. Satz des Pythagoras stellt traditionell eine merkwürdige Schaltstelle im Unterricht der Sekundarstufe I dar: Es ist für Schüler bei der Erstbegegnung ein wesentlich theoretischer, scheinbar exotischer Lehrsatz, der sich mangels schülernaher Probleme echten Nacherfindungsansätzen widersetzt, wenn man von suggestiven Lehrerhilfen absehen möchte. Warum sollte sich überhaupt wer für so eine quadratische Beziehung an speziellen Dreiecken interessieren? Entsprechend schwierig ist erfahrungsgemäß, ihn 14- oder 15-jährigen Schüler/Inne/n mit allerlei Versprechungen "für später" halbwegs bedeutungsgerecht nahe zu bringen. (Vgl. dazu H.W. Heymanns (damals gescheiterten) Vorschlag von 1996, den Pythagoras-Satz in manchen Schulformen aus dem Pflichtprogramm zu nehmen. (Näheres s.u. bei den Rezensionen bzw. unter: Link)
2012	Nicht jeder ist seines Glückes Schmied – Sozialkundliches im einstigen Mathematikunterricht. In: Der Mathematikunterricht, Heft 4/2012, S. 4-25. (Näheres s. hier.) Schwerpunkt: Hundert Jahre Bemühen im MU um Beschreibende und Schließende Statistik anhand (gesellschaftlich) relevanter Daten – mit sehr wechselhaftem und durchweg eher bescheidenem Erfolg ...
2012	Elementare Näherungskonstruktionen für regelmäßige Vielecke (Studien zu einem Festvortrag für Günter Pickert am 29. Juni 2012; unveröff. 119-seitiges Manuskript vom August 2014.) Schwerpunkte: 1. Einfache Fälle; 2. Strategien am regulären Fünfeck; 3. Theoretisch �exakte� Fünfecks-Konstruktionen; 4. Fast-reguläre Siebenecke; 5. Fast-reguläre Neunecke; 6. Fast-reguläre Elfecke; 7. Fast-reguläre Dreizehnecke; 8. Höhere n-Ecke � Fortgesetzte Bogenhalbierung und Projektionsmethoden; 9. Näheres zur Nicht-/Konstruierbarkeit im klassischen Sinne.
2014	YBC 7289 - Didaktische Spekulationen zu einer Keilschrifttafel und zur Kultur der altbabylonischen (Sekundar-) Mathematik (Vortrag) Schwerpunkt: Welche Erkenntnisinteressen führten zum sogenannten "Satz des Pythagoras"? (Schlussfolgerungen zu den Untersuchungen von 2011, s.o.; Näheres auf Anfrage.)
2015-...	Algebra als Pflicht für alle?? (laufendes Projekt) Schwerpunkt: Welche didaktischen oder gesellschaftlichen Gründe könnten pflichtmäßigen Algebraunterricht auch für jene Mittelstufen-Schüler/Innen rechtfertigen, die Algebra jenseits der Schule ganz offensichtlich nicht mehr brauchen werden? Verdacht: Die bestehenden Vorschriften und Lehrer-Ausbildungsformen beantworten die Fragen nicht wirklich, obwohl es sich um eine deutliche Mehrheit von Betroffenen handeln dürfte... (Zwischenergebnisse auf Anfrage.)
2019	Mit Weite oder Tiefe zum Pythagoras-Satz? - Sehr, sehr Altes zum Einstieg heute (Unveröff. Manuskript, 15 S., Näheres auf Anfrage.) Schwerpunkt: Der aus ältesten Überlieferungen bekannte Pythagoras-Satz mit seinen erstaunlichen Funktionen in allen heutigen Schwerpunktgebieten der weiterführenden Schulmathematik stellt ein besonderes pädagogisches Problem dar: Wie kann Schülern bei seiner Ersteinführung eine Ahnung davon vermittelt werden, dass er wie keine andere Beziehung alles präzise Wissen und Nachdenken über Nichtlineares direkt oder indirekt (mit-)prägt? Dazu kamen dem - erst sehr viel später sogenannten - Pythagoras-Satz seit der altbabylonischen Schreiberkaste immer wieder auch Ausweisfunktionen für ständisches Insiderwissen zu. (Heute etwa vergl. mit aktuellen IT-Kenntnissen...)

*Unterrichtsmethodisches zum MU der Sekundarstufen*
1983	Geometrieunterricht in einer 7. Klasse ( Geometrie aus der Tiefe (1983))
1984	Widersprüche und Trugschlüsse als Unterrichtsmittel. In: Mathematik lehren, Heft 5, S. 44-49. (Gemeinsam mit S. Gey und L. Westermann.) Schwerpunkt: Beschreibung von drei Unterrichtsstunden zur Elementargeometrie mit produktiver Fehlernutzung (Winkelsumme im Dreieck, Spiegelungen).
1984	Das Ende vom Lied: Korrekturen und Berichtigungen. In: Mathematik lehren, Heft 5, S. 22-24. Schwerpunkt: Das Niveau von Unterricht wird im Unterricht erzeugt, nicht in Klausuren oder Tests, die bekanntlich viele Schüler und Lehrer eher demotivieren. Allerdings dämpfen formelle Leistungskontrollen auch Selbstüberschätzungen – ebenfalls auf Schüler- und Lehrerseite.
1996	Wurzeln, Mathematik und Nostalgie – Bedenkliches zum mathematischen Wagenschein. In: G. Pospiech, F. Siemsen, T. Görnitz (Hrsg.): Staunen, Fragen, Verstehen - Tagung zum 100. Geburtstag Martin Wagenscheins. Frankfurt: Inst. für Didaktik der Physik 1998, S. 151-174. ( Manuskript) Schwerpunkt: Wagenscheins zeitgenössische Kritik am landläufigen apodiktischen MU und sein vehementes Eintreten für sokratisches Lehren werden gewürdigt. Leider genügten, so die hier vertretene Ansicht, Wagenscheins berühmteste Unterrichtsbeispiele zum MU den eigenen Forderungen nur teilweise. (Vgl. auch die Abschnitte 5.1 und 6.3 sowie die Anhänge A-5.1.1/2 im Buch Päd. des MU. - Einige Wagenschein-Verehrer bestritten meine Einwände teils verdeckt, teils offen. Zu letzterem s. z. B. Link)
2000	Gruppenarbeitsbeispiel zur Gestalt- und Volumenbestimmung eines schiefen Polyeders Link.
2004	Fehler als Orientierungsmittel. In: Mathematik lehren, Heft 125, S. 3-8. (Zusammenfassung erschien in: Beiträge zum MU. Hildesheim: Franzbecker 2004, S. 181-184.) Schwerpunkt: "Der Beitrag gibt als Einführung in das Themenheft 'Fehler als Orientierungsmittel' einen Überblick über typische Schülerfehler in einigen Sachgebieten der Mathematik und regt an, die Fehlerdämpfung bei Mathematisierungen unterrichtsmethodisch mit konstruktiver Fehlernutzung zu verbinden, sie also wesentlich in die Schulmathematik einzubeziehen." (Abstract vom Fachportal-Pädagogik.de) Der Aufsatz ist als Ergänzung zum Basisartikel über Fehlerforschung von 1984 gedacht.

*Grundsätzliches zum MU und zur mathematikdidaktischen Lehrerausbildung*
1981	Zur Entstehung und Begründung des Analysisunterrichts an allgemeinbildenden Schulen. In: Der Mathematikunterricht 27.5, S. 81-222. Vgl. dazu die aktuellere und gründlichere Untersuchung: Verstehen oder Berechnen?? Wie passt der Computer zum Analysisunterricht des 20. Jahrhunderts? Erschienen 2012 im Tagungsbericht 2008/09 des AK MUI, S. 103-136. (S. o. gegen Ende der Rubrik "Fachmethodisches zum MU der Sek. II". Online-Version: Link.)
1988	Pflichtbindung verpflichtet – zur Säkularisierung der Mathematik in der Sekundarstufe II. In: Festschrift für Heinrich Winter. Paderborn: Schöningh, S. 48-56. Schwerpunkt: Begriffsfelder der Anwender von Mathematik sind besser für die Schule geeignet als die strenge Begriffswelt der Reinen Mathematiker. („Formale Anwendungsorientierung“; vgl. Abschnitt 7.2: „Anwendungsorientierung der Mathematik“in "Päd. des MU".)
1988	Mattematik – Laterna magica der Späth-Renaissance. In: Festschrift - Staatliches Studienseminar Hameln – 1978-1988, S. 87-104. Link Schwerpunkt: Mit welchen Begründungen ließen oder lassen sich die kanonischen Gegenstände des MU auf den Sekundarstufen gegenüber einer breiteren Öffentlichkeit (von Steuerzahlern oder Steuerern) rechtfertigen?
1997	Leserbrief zur Gymnasiallehrerausbildung in Mathematik. In: DMV-Nachrichten, Heft 4, S. 49-51. Manuskript Schwerpunkte: Kritik an Tendenzen zur Fachlastigkeit, Schulferne und zu Bedeutungsverzerrungen.
1997	Pädagogik des Mathematikunterrichts. Wiesbaden: Vieweg. (300 S.). ( Korr. Manuskript 2012/2018.) Schwerpunkte: Kritische Überblicke für Lehrer/Innen und Lehramtsstudierende zu Unterrichtsformen und didaktischen Orientierungen sowie zur Lehrerrolle; Sammlung von Quellenzitaten. (ZDM-Rezension von Th. Jahnke.)
1997	Sieben Jahre Mathematik sind vermutlich nicht genug. In: Beiträge zum MU, S. 147-150. Schwerpunkt: Konstruktive Kritik der Heymann-Perspektiven. (Kurzfassung der folgenden Aufsatzserie:)
1998	Mathematikunterricht nach dem 7. Schuljahr – Warum eigentlich für alle? In: Mitteilungen Math. Ges. Hamburg 17, S. 15-49. Etwas gekürzte und aktualisierte Fassung in: Neue Sammlung, 38.4 (1998), S. 489-511. (Manuskript unter Link.) - Weitere Kurzufassungen in: H. Althoff (Hrsg.): Berichte aus dem Seminar für Didaktik der Mathematik. Bielefeld: Universität WS 97/98 bis SS 98, S. 39-46. Schwerpunkt: Es wird vorgeschlagen, den weiterführenden MU - nach Bürgerlichem Rechnen und Beschreibender Statistik - auf Denkfiguren im kollektiven Bewusstsein („metaphorische Bedeutungen“), spezifische Erkenntnisweisen („epistemologische Kraft“) und/oder Aufklärungsfunktionen („emanzipatorisches Potential“) zu konzentrieren.
2000	Dreihundert Jahre Theorie des öffentlichen Mathematikunterrichts in Deutschland. In: Beiträge zum Mathematikunterricht 2000. Hildesheim: Franzbecker 2000, S. 19-26. ( Manuskript dieser Kurzfassung oder auch längeres Manuskript mit Hintergrundmaterialien und Quellennachweisen.) Schwerpunkt (vgl. Kurzfassung): In einem kursorischen Überblick wird versucht, traditionelle, bis heute maßgeblich fortwirkende Prägungen des MU und der MaDi zu identifizieren: 1. Schule und Ökonomie, 2. Religiöse Hintergründe, 3. Gesellschaftsnutzen, 4. Methodische Sorgfalt, 5. Moralerziehung durch Mathematik.
2002	Effizienz oder Substanz? – Pädagogische Überlegungen zum MU, Ausarbeitung eines Vortrags, Ingolstadt 2001. In: K. Röttel (Hrsg.): Mathematik, nützlich und schön – vor 500 Jahren und heute. Eichstätt: Polygon 2002, S. 85-112. (s. a. Kurzvortrag dazu, Weingarten 2000.) Es wird versucht, die innere Widersprüchlichkeit und Unaufrichtigkeit des Effizienz- oder "Kompetenz"ansatzes aufzuzeigen. Die Rahmenbedingungen, unter denen effizienzgesteigerter Mathematikunterricht stattfindet bzw. stattfinden wird, zwingen wieder den alten Wein in alte Schläuche und sorgen lediglich für neue Etiketten. Wirklich zeitgemäßer oder gar zukunftsweisender Mathematikunterricht wird dadurch nicht gefördert, sondern massiv behindert, weil er durchgreifende und darum riskante Veränderungen in der traditionellen Mathematikauffassung, -ausbildung und -gewichtung verlangen würde. Schwerpunkte: 1. Wollten die in unserem Lande bildunsgpolitisch Verantwortlichen den Schulbetrieb tatsächlich effektivieren, dann böte sich eine ganze Reihe von kostenneutralen oder sogar kostendämpfenden betrieblichen Verbesserungen nach Vorbildern aus anderen Kulturländern an. 2. Bemühungen um Lehrermotivation würden sinnvoller wirken als Inszenierungen oder Bonbons zur Schülermotivation. 3. Math.-naturw. Unterricht sollte explizit demokratisch legitimiert werden. Dem entspräche ein zu verhandelndes Wissen und Wollen als gesellschaftliches Konstrukt ("formale Anwendungsorientierung"; vgl. Abschnitt 7.2 in "Päd. des MU") sehr viel besser als permanentes Herunterarbeiten irgendeines "Qualifikationen-Katalogs" (statistische Kompetenzorientierung)zur Dressur auf positives Verfügungswissen, -können und jederzeitige Abrufbarkeit.
2002	Über einige Grundfragen künftiger Geometriedidaktik. In: Mathematica didactica 25.1, S. 55-78. Online unter: Link. (Kurzfassung dazu: Über einige Desiderate der Geometriedidaktik. In: Beiträge zum MU 2002. Hildesheim: Franzbecker 2002, 175-178. Manuskript.) Schwerpunkte: Folgt man der Auffassung, dass Geometrieunterricht an allgemeinbildenden Schulen vor allem zwei Ziele zu verfolgen hat, nämlich die Wahrnehmung im Anschauungsraum und Heuristiken des Problemlösens zu fördern, dann ergibt sich daraus eine Reihe von noch ungelösten oder zumindest unbefriedigend gelösten Aufgaben: Allgemeiner Geometrieunterricht sollte die Beziehungen zwischen ebener und Raumgeometrie aus didaktischer Sicht klären, geometrische Fachsprache und Umgangssprache im Unterricht verschmelzen statt gegeneinander absetzen, Begriffswissen säkularer begreifen und Elementargeometrie � auch � als Sprache für Bewegungsvorgänge und Prozesse entwickeln.
2005	Kleine Revue sozialer Aspekte der Schulgeometrie. In: Der Mathematikunterricht 51.2/3, S. 70-85. (Manuskript dazu s. hier.) Schwerpunkt: Eine kritische Analyse des Zeitgeistes in den KMK-Standards am Beispiel Geometrie, "weil sie lange zum Geistreichsten zählte, das man allgemeiner Volksbildung zutrauen wollte". Daran soll aufgezeigt werden, "dass objektivierte Qualitätssicherungsmassnahmen die unterschwellige Tendenz haben, das Soziale aus einer wünschenswerten mathematischen Allgemeinbildung ins Private und Unverbindliche lokaler Unterrichtsmethodik abzuschieben". Zur Erläuterung wird auf historische Überlegungen und Beispiele zurückgegriffen, an denen u.a. deutlich werden soll, dass ein Mathematiklehrer unvermeidlich verschiedene Rollen spielen muss, dass er aber tagtäglich, gewollt oder ungewollt, seine eigenen Akzente wählt und (nach-) wirken lässt. (Leicht geändertes Abstract aus Fachportal-Pädagogik.de.)
2008	Geometrieunterricht abstrakt - ... (Auführliche Vortragsausarbeitung zur folgenden Veröffentlichung:)
2009	Vom Begründensollen zum Vermutenwollen. In: M. Ludwig, R. Oldenburg, J. Roth (Hrsg.): Argumentieren, Beweisen und Standards im Geometrieunterricht. AK Geometrie 2007/08. Hildesheim: Franzbecker 2009, S. 167-188. (Online unter: Link; dort pdf-Seiten 171-192. - Schwerpunkt: Ziel des allgemeinen Unterrichts auf den Sekundarstufen kann wegen ihrer zunehmenden Einschmelzung ("Enttypisierung"), Bürokratisierung und inneren Diversifizierung nicht mehr das Beweisenlernen sein. Der an sich wünschenswerten Verbreiterung und Demokratisierung der Bildungsbeteiligung könnte mehr Bescheidenheit durch Konzentration auf eine Erziehung zum Vermuten- und Argumentierenwollen besser entsprechen.
2007/2009	Was könnte zeitgemäßer Mathematikunterricht zu naturwissenschaftlicher Allgemeinbildung beitragen? (Ausarbeitung eines Vortrags vom Juni 2007 bei der Eröffnung des Zentrums für mathematisch-naturwissenschaftliche Bildung an der Kölner Universität sowie kurz danach auf der AK Geo-Tagung in Königswinter.) In: M. Ludwig, R. Oldenburg, J. Roth (Hrsg.): Argumentieren, Beweisen und Standards im Geometrieunterricht. AK Geometrie 2007/08. Hildesheim: Franzbecker 2009, S. 11-52. (Online unter: Link, dort pdf-S. 6 f. und 15 ff.) Schwerpunkte: Ausführliche Kritik des Neobehaviorismus in der akademischen Forschungsdominanz und Politikberatung der Empirischen Unterrichtsforschung. Plädoyer für einen durchgehenden Unterrichtsschwerpunkt „kritisches Modellbilden“ mit gründlicher Reflexion der unvermeidlichen Perspektivwahl-, Theorie- und Interpretationsanteile.
2012	Nicht jeder ist seines Glückes Schmied – Sozialkundliches im einstigen Mathematikunterricht. In: Der Mathematikunterricht, Heft 4/2012, S. 4-25. (Manuskript auf Anfrage; 5-seitiges Quellenverzeichnis s. Link.) Schwerpunkt: Hundert Jahre Bemühen im MU um Beschreibende und Schließende Statistik anhand (gesellschaftlich) relevanter Daten – mit sehr wechselhaftem und durchweg eher bescheidenem Erfolg ...
2016	nutzloser Leserbrief Link. Schwerpunkt: Das heutige Schulwesen disqualifiziert den Lehrerberuf.
2019	Mit Weite oder Tiefe zum Pythagoras-Satz? - Sehr, sehr Altes zum Einstieg heute (Unveröff. Manuskript, Näheres auf Anfrage.)

*Allgemein Mathematikdidaktisches*
1983	Geometrieunterricht in einer 7. Klasse ( Geometrie aus der Tiefe (1983))
1984	Ich denke, also irre ich - Anfänge und Grenzen der Fehlerkunde. In: Mathematik lehren, Heft 5, S. 2-9. Schwerpunkte: Überblick zur Fehlerforschung bzgl. des MU. - Fehler, die nicht einfach (unregelmäßig auftretende) Flüchtigkeitsfehler sind, können und sollten im MU konstruktiv genutzt werden. Fehlerprävention ist dagegen ein heikles Ziel, weil stets Verwirrung droht und Fehlermuster sehr häufig labil sind. Auch die leider gängige Leistungseinschätzung nach Fehlerquoten wirkt tendenziell kontraproduktiv, nämlich bürokratisierend und sinnentleerend statt zum Wagnis des Selberdenkens ermutigend. (Vgl. oben zum Stichwort "Unterrichtsmethodisches" den ml-Basisartikel "Fehler als Orientierungsmittel" von 2004.)
1985	„Funktionales Denken“: Bewegtes fassen – das Gefaßte bewegen. In: Mathematik lehren, Heft 11, S. 12-13. Schwerpunkt: Funktionales Denken ist mehr und teilweise anderes als technische "Kompetenz" im Umgang mit mathematischen Gegenständen namens "Funktionen" oder "Zuordnungen". Plädoyer für die Betonung changierender Variablenbezüge. (Vgl. auch die Arbeit zur Analysis-Didaktik „Verstehen oder Berechnen“ von 2012; s. o. in der Rubrik "Fachmethodisches zum MU der Sek. II".)
1985	Rechner im Mathematikunterricht. In: Mathematik lehren, Heft 13, S. 2-3. Schwerpunkt: Rat zur Gelassenheit angesichts der aufkeimenden Forderungen nach Computerorientierung. (Mit ein paar schönen Voraussagen der inzwischen eingetretenen Entwicklung.)
1986	Anwendungsorientierung der Mathematik aus geschichtlicher Sicht. In: Mathematik lehren, Heft 19, S. 42-48. Schwerpunkt: Versuch, historische Belege zur konstitutiven Rolle von Anwendungen für die Entwicklung der schulrelevanten wissenschaftlichen Mathematik zu finden.
1991	Bericht über die 10. Tagung der Fachleiter für Mathematik an den Seminaren für Lehrerausbildung in der Bundesrepublik Deutschland (Hrsg.). Schriften des Deutschen Vereins zur Förderung des math. und naturw. Unterrichts, Heft 47. Schwerpunkt: Rahmenthema der Tagung war die Frage, inwiefern tatsächliche Anwendermathematik(en) jenseits der Schule Anwendungsorientierung des MU rechtfertigen.
1994	Störungen der Mathematikdidaktik durch die Realität. (Antrittsvorlesung Goethe-Universität Frankfurt am Main) Manuskript Schwerpunkt: Berücksichtigt man die institutionellen und tradierten Rahmenbedingungen, unter denen MU tatsächlich stattfindet (sog. „Instituetik“; nach S. Bernfeld: s. Zitat im Anhang des Manuskripts), dann werden erhebliche Lücken und Blickverengungen in Mathematikdidaktik und Lehrerausbildung deutlich.
1997	Pädagogik des Mathematikunterrichts. Wiesbaden: Vieweg. (300 S.). ( Korr. Manuskript 2018.) Schwerpunkte: Kritische Überblicke für Lehrer/Innen und Lehramtsstudierende zu Unterrichtsformen und didaktischen Orientierungen sowie zur Lehrerrolle; Sammlung von Quellenzitaten. (ZDM-Rezension von Th. Jahnke.)
1999	"Design Science" als dynamisierte Wissenschaftsmethodik und Sozialform innerhalb der Mathematikdidaktik. In: C. Selter/G. Walther (Hrsg.): Mathematikdidaktik als design science – Festschrift für E.C. Wittmann, Leipzig: Klett, S. 78-85. Schwerpunkt: Das Dortmunder Projekt „mathe 2000“ wird als zyklische Entwicklungforschung unter gleichberechtigten Theorie-Praxis-Teams interpretiert. Auf S. 82 f. im Festband-Aufsatz wird das an einem Projektentwurf zum Thema "Verhältnisse" illustriert.
1999	Wem nützt Mathematikdidaktik? In: W. Kaunzner (Hrsg.): Lehren und Lernen – Festschrift zum 60. Geburtstag von Karl Röttel, Buxheim: Polygon-Verlag, S. 78-81. ( Manuskript) Schwerpunkte: 1. MaDi nützt (angeblich) dem MU; 2. akademische MaDi nützt sich selbst und der Hochschulmathematik; 3. MaDi schafft eine informelle Sprache und dadurch Modellbewusstsein; 4. MaDi soll(te auch) dem öffentlichen Diskurs über mathematische Lernprozesse dienen.
2000	"Formale Anwendungsorientierung" (Vortragsmanuskript) Link Schwerpunkt: Konkretisierung von Abschnitt 7.2 der "Päd. des MU" von 1997.
2002	Über einige Grundfragen künftiger Geometriedidaktik. In: Mathematica didactica 25.1, S. 55-78. Online unter: Link. (Kurzfassung dazu: Über einige Desiderate der Geometriedidaktik. In: Beiträge zum MU 2002. Hildesheim: Franzbecker 2002, 175-178. Manuskript.) Schwerpunkte: Folgt man der Auffassung, dass Geometrieunterricht an allgemeinbildenden Schulen vor allem zwei Ziele zu verfolgen hat, nämlich die Wahrnehmung im Anschauungsraum und Heuristiken des Problemlösens zu fördern, dann ergibt sich daraus eine Reihe von noch ungelösten oder zumindest unbefriedigend gelösten Aufgaben: Allgemeiner Geometrieunterricht sollte die Beziehungen zwischen ebener und Raumgeometrie aus didaktischer Sicht klären, geometrische Fachsprache und Umgangssprache im Unterricht verschmelzen statt gegeneinander absetzen, Begriffswissen säkularer begreifen und Elementargeometrie � auch � als Sprache für Bewegungsvorgänge und Prozesse entwickeln.
2015	Stellungnahme zu Gert Schubrings erfreulich pointierter Kritik "der" stoffdidaktischen Tradition. In: GDM-Mitteilungen 99, S. 23-25. Schwerpunkt: Plädoyer für eine weniger wissenschaftsfixierte, breitere und offenere "Stoffdidaktik" als (ein) konstitutives Teilgebiet der Mathematikdidaktik.

*Geschichtliches zu Schulmathematik und Mathematikunterricht*
1981	Zur Entstehung und Begründung des Analysisunterrichts an allgemeinbildenden Schulen. In: Der Mathematikunterricht, 27.5, S. 81-222. (Vgl. dazu die neuere und gründlichere Untersuchung: Verstehen oder Berechnen? Wie passt der Computer zum Analysisunterricht des 20. Jahrhunderts? Erschienen 2012 im "Tagungsbericht 2008/09 des AK MUI"; S. 103-136; s. Link.)
1981	Zum Gehalt der elementaren Integralrechnung in ideengeschichtlicher Sicht. In: Der Mathematikunterricht, 27.5, S. 7-60. Schwerpunkt: Wandlungen „der“ schulrelevanten Integralbegriffe.
1986	Anwendungsorientierung der Mathematik aus geschichtlicher Sicht. In: Mathematik lehren, Heft 19, S. 42-48. Schwerpunkt: Versuch, historische Belege zur konstitutiven Rolle von Anwendungen für die Entwicklung der schulrelevanten wissenschaftlichen Mathematik zu finden.
1991 1992	Historical Stories in the Mathematics Classroom. In: For the Learning of Mathematics, Vol. 11., S. 24-31. Etwas geändert auch in: The mathematical gazette, Vol. 76, No. 475, 1992, S. 127-138. (Online unter: Link.) Schwerpunkt: Historisch plausible Geschichten können mathematisches Denken, Entdecken und Argumentieren paradigmatisch nacherfinden lassen. Dabei können Respekt vor überzeitlichen Leistungen vermittelt und intertemporäre Heuristiken gelernt werden. Das wird an (modernisierten) Geschichten zur Kreis- und Erdumfangsmessung illustriert; im Text von 1991 zusätzlich an der Entdeckung der cardanischen Formel. (Vgl. auch das von mir 1986 herausgegebene Heft 19 von Mathematik lehren „Geschichte –Geschichten“ sowie den nächsten Text:)
1996 2001	Kubische Gleichungen und die widerwillige Entdeckung der komplexen Zahlen. (S. o. Link.)
1997	Zur frühen Feldmessung. In: Mathematica didactica 20.1, S. 20-25. Schwerpunkt: In alten Kulturen wurden viereckige Felderflächen wie Rechtecke mit Seiten berechnet, die sich als Mittelwerte von Gegenseiten ergaben. Wie gut ist das?
1999 2000	Dreihundert Jahre Theorie des öffentlichen Mathematikunterrichts in Deutschland. In: Beiträge zum MU. Hildesheim: Franzbecker 2000, S. 19-26. Manuskripte. Schwerpunkt: In einem kursorischen Überblick wird versucht, traditionelle, bis heute maßgeblich fortwirkende Prägungen des MU zu identifizieren.
2003	Die Erdmessung des Poseidonios, hermeneutische Skrupel und mathematical literacy. In: Journal für Mathematik-Didaktik, Bd. 24 (2003), Heft 3/4, S. 236-251. (Gedanken zu einem JMD-Aufsatz von M. R. Glaubitz und H. N. Jahnke. Anschließende Erwiderung dieser Autoren, ebenda S. 252-260.) Schwerpunkt: "Anhand einiger Detailüberlegungen zur Parallelitaet von Sternenlicht und zur Frage nach der Genauigkeit von Poseidonios' Erdumfangsbestimmung, wird die Auffassung vertreten, dass historische Quellentexte, ihre Autoren und Bezugspersonen Mittel des Mathematikunterrichts bleiben sollten, nicht Untersuchungsgegenstaende. Jeder Versuch, solche Texte eindeutig oder gar mit heutigem, meist auch nur geglaubtem Wissen 'besser zu verstehen' als ihre Autoren selbst, wie es Dilthey der Hermeneutik ins Gesangbuch geschrieben hat, setzt mehr historischen Takt voraus als Schülern zumutbar ist, die noch mit den damals schon reflektieren Phänomenen selbst ihre Not haben. (Autorenreferat)" (Abstract aus Fachportal-Pädagogik.)
2005	Geniale Ideen und ein lehrreicher Fehler des berühmten Herrn Galilei. In: Mathematica didactica 28.1, S. 58-78. Schwerpunkt: Lehrreiche Hindernisse bei der Entdeckung der Brachistochrone.
2006	Heuristik und Geschichte der elementaren Volumenberechnung. In: Mathematica didactica 29.1, 69-101. Online unter: Link. Schwerpunkt: Welche Typen von Raumkörpern können im Rahmen des MU der Sek. I sinnvoll so beschrieben und berechnet werden, dass nebenbei auch Sek. II-Geometrie vorbereitet wird? Als heuristisch besonders fruchtbar haben sich dafür - auch historisch - Ähnlichkeitsbetrachtungen und das Cavalieri-Prinzip (verallgemeinerte Scherungen) erwiesen. Wenn die Versicherung der Lehrerin oder des Lehrers atmosphärisch ausreicht, das Cavalieri-Prinzip funktioniere für die behandelten Körper in der Sek. I garantiert problemlos, kann durchaus auch an Schwierigkeiten (Paradoxien) der schichtenweisen Dimensionsreduktion herangeführt werden und so ein Motiv für spätere definitorische Mühen mit dem Integralbegriff bereitgestellt werden.
2009	Verstehen oder Berechnen? Wie passt der Computer zum Analysisunterricht des 20. Jahrhunderts? Erschienen 2012 im "Tagungsbericht 2008/09 des AK MUI", S. 103-136; s. Link. Schwerpunkte: Entwicklung derAnalysisdidaktik im 20. Jh.; instituetische und bildungspolitische innere Widersprüche; aktuelle Begründungsnöte; Plädoyer für Datenmodellierung als durchgängige Leitidee für beide Sekundarstufen.
2012	Nicht jeder ist seines Glückes Schmied – Sozialkundliches im einstigen Mathematikunterricht. In: Der Mathematikunterricht, Heft 4/2012, S. 4-25. (Zugang s. hier) Schwerpunkt: Hundert Jahre Bemühen um Beschreibende und Schließende Statistik im MU anhand relevanter Daten – mit sehr wechselhaftem und durchweg eher bescheidenem Erfolg.
2014	Näheres zu YBC7289. (Unveröff. Manuskript.) Schwerpunkt: Die altbabylonische Keilschrifttafel YBC7289 (1. Drittel des 2. Jtd. vor Chr.) zeigt ein Quadrat mit seinen Diagonalen und erstaunlich gute Näherungswerte für das Diagonalen-Seiten-Verhältnis. Neuere Forschungen von Altorientalisten und spezialisierten Mathematikhistorikern lassen vermuten, dass der ursprüngliche Sinn und einige denkbare Methodenquellen dieser Beschriftungen aus fachlichen Spezialisierungen und Überhöhungen in den ökologisch notwendigen Schreiberschulen (Verwaltungsschulen) des Alten Irak stammten. (S. a. den Aufsatz "Wege zum Pythagoras-Satz" Link.)
2019	Mit Weite oder Tiefe zum Pythagoras-Satz? - Sehr, sehr Altes zum Einstieg heute (Unveröff. Manuskript, Näheres auf Anfrage.)

*Rezensionen*
1981	Rezension von „Anschauliche Analysis“ (Bayer. Schulbuchverlag). In: Zentralblatt für Didaktik der Mathematik 1981, Heft 3, S. 87-97. Fazit: Sinnvoller Theorieaufbau von der grenzwertfreien Behandlung der Ableitungen rationaler Funktionen zu Grenzwertbetrachtungen für tranzendente Funktionen.
1982	Rezension der „DIFF-Studienbriefe Analysis“. In: Zentralblatt für Didaktik der Mathematik, 1982, Heft 3, S. 163-167.
1984	Rezension von: W. Blum/G. Törner: Didaktik der Analysis. In: Zentralblatt für Didaktik der Mathematik 1984, Heft 4, S. 132-138. Kritik: Vernachlässigung von Bedeutungsfragen aus Schülersicht.
1995	Rezension von: S. Müller-Philipp: Der Funktionsbegriff im Mathematikunterricht (Rezension). Zentralblatt für Didaktik der Mathematik, 1995, Band 4, S. 127-129. Kritik: Konflikt zwischen konzeptionellem Begriffserwerb und Testanliegen.
1997	Von der Entsorgung mathematischer Bildung durch ihre Theorie (Rezension und Kommentar zu H. W. Heymann: Allgemeinbildung und Mathematik. Weinheim 1996). In: Zentralblatt für Didaktik der Mathematik, 1997, Heft 2, S. 53-61. Online unter: Link.
1998	Rezension von: Tietze/Klika/Wolpers: Mathematikunterricht in der Sekundarstufe II, Band 1. In: Zentralblatt für Didaktik der Mathematik 1/1998, S. 7-11. Online unter: Link Tendenz: Gute Überblicke, vor allem im Analysisteil.
2004	Rezension von: H.-W. Henn: Elementare Geometrie und Algebra. In: Zentralblatt für Didaktik der Mathematik 36.2 (2004), S. 82-84. Online unter: Link Tendenz: Rein innermathematische Sicht auf schulrelevante "Mathematik vom höheren Standpunkt".
2010	Rezension von: P. Ullmann: Mathematik – Moderne – Ideologie (Konstanz: UVK 2008, 314 S.). In: Mitteilungen der Gesellschaft für Didaktik der Mathematik 89 (2010), S. 74-76. Online unter: Link Tendenz: Die soziologisch-kritische Sicht des Buches würde die heute leider zunehmend technologische MaDi sehr bereichern.

-	schulmathematische Fach- und/oder Unterrichtsmethodik; vgl. etwa das Konzept zum Lehrbuch Päd.des MU von 1997
-	Geschichte der schulrelevanten Mathematik und des Mathematikunterrichts; s. z. B. die Kurzfassung zum GDM-Hauptvortrag von 2000 oder auch die eigentliche Ausarbeitung.
-	mathematikdidaktische Grundsatzfragen (Legitimationen, Gesellschaftsbezug, Erziehungsfunktionen, Leitideen, Wissenschaftstheorie, ...); vgl. etwa meine Frankfurter Antrittsvorlesung von 1994, den Leserbrief "Leere Lehre" von 2009 oder auch den nutzlosen Leserbrief von 2016