Statistisches Praktikum im SS 2022

Prof. Dr. Gaby Schneider, unter Mitarbeit von Solveig Plomer und Fabian Roth

Seminar im SS 2022. Do. 12:30 Uhr, 711 groß.

Thema 1: Statistische Methoden zur Diabetes-Früherkennung

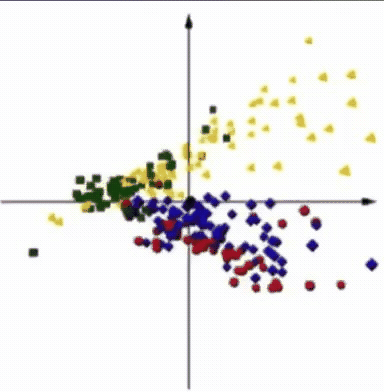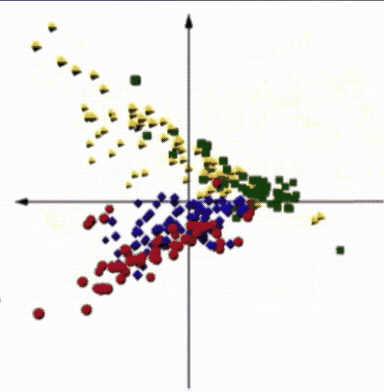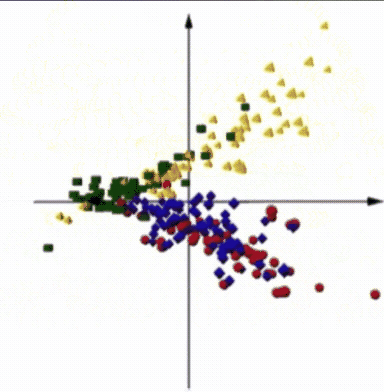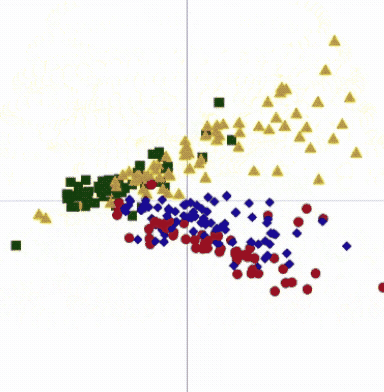
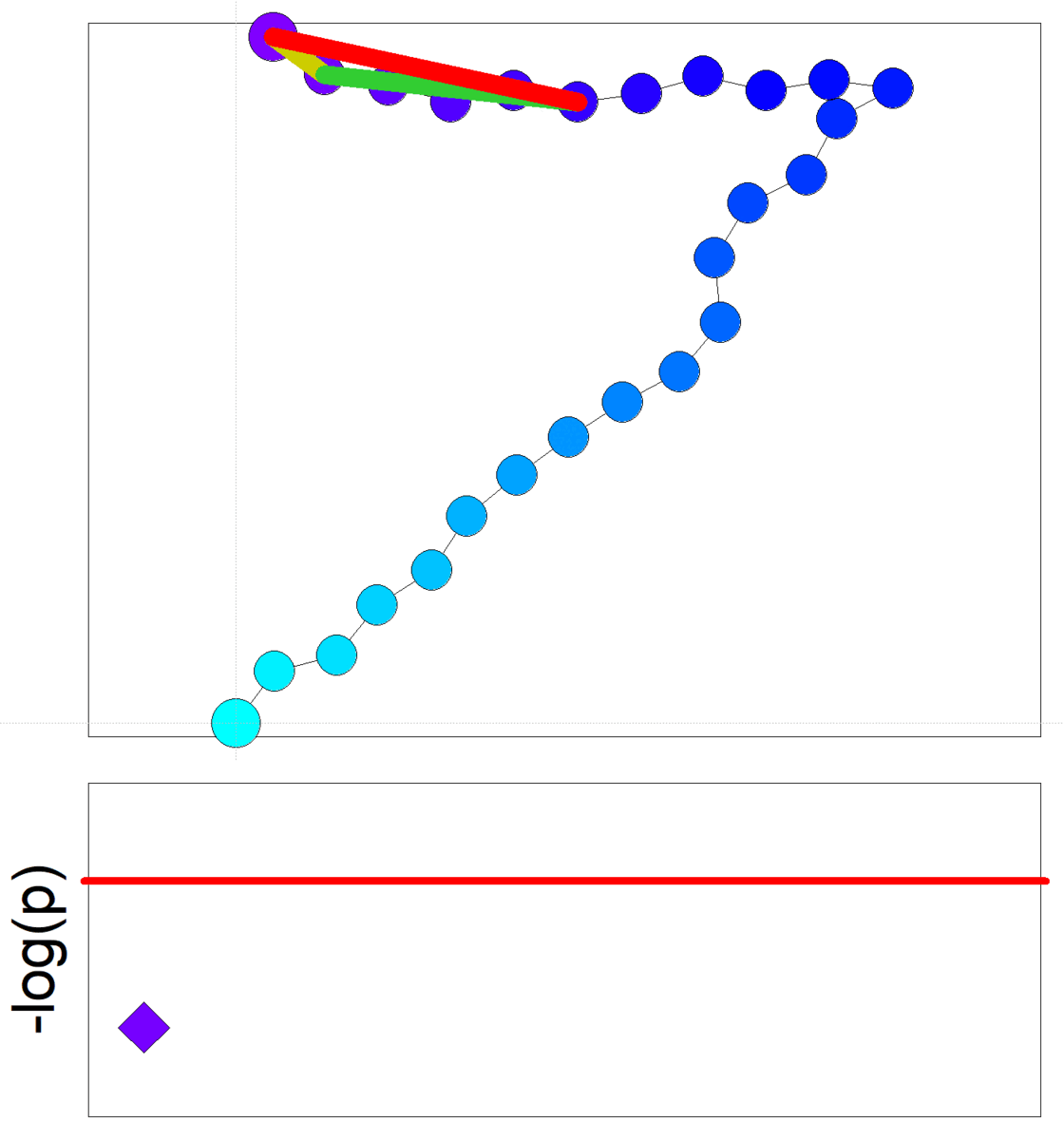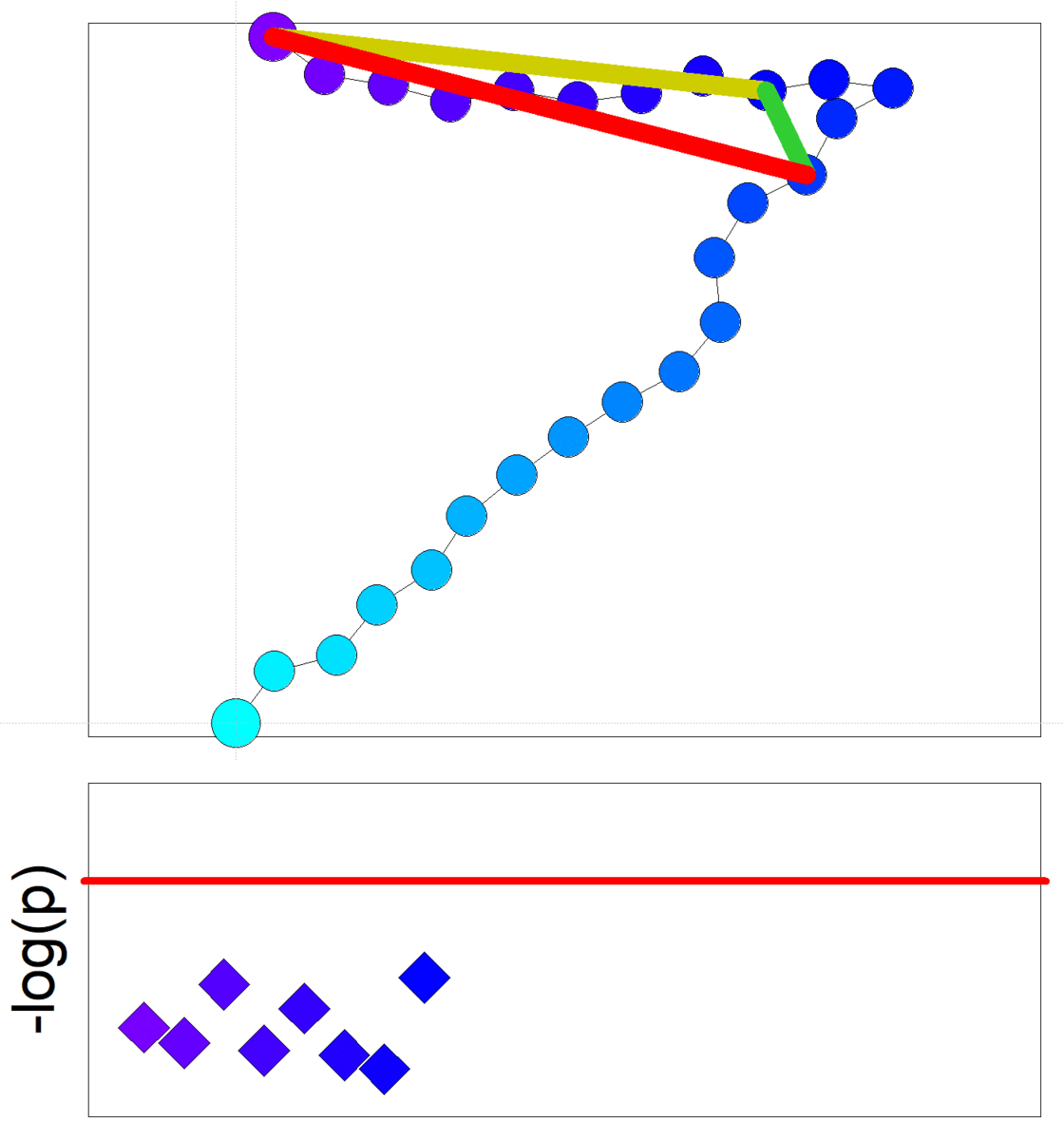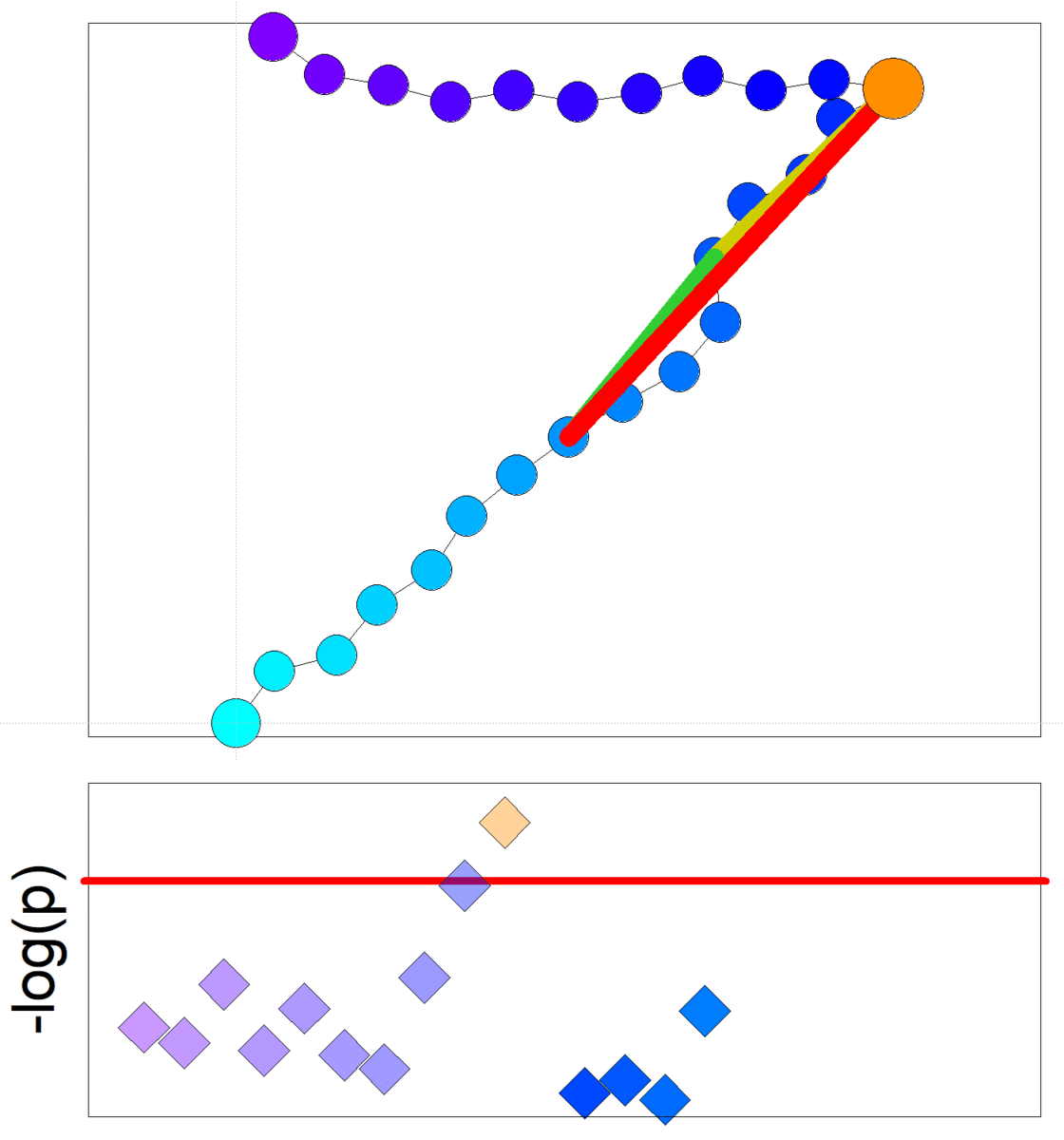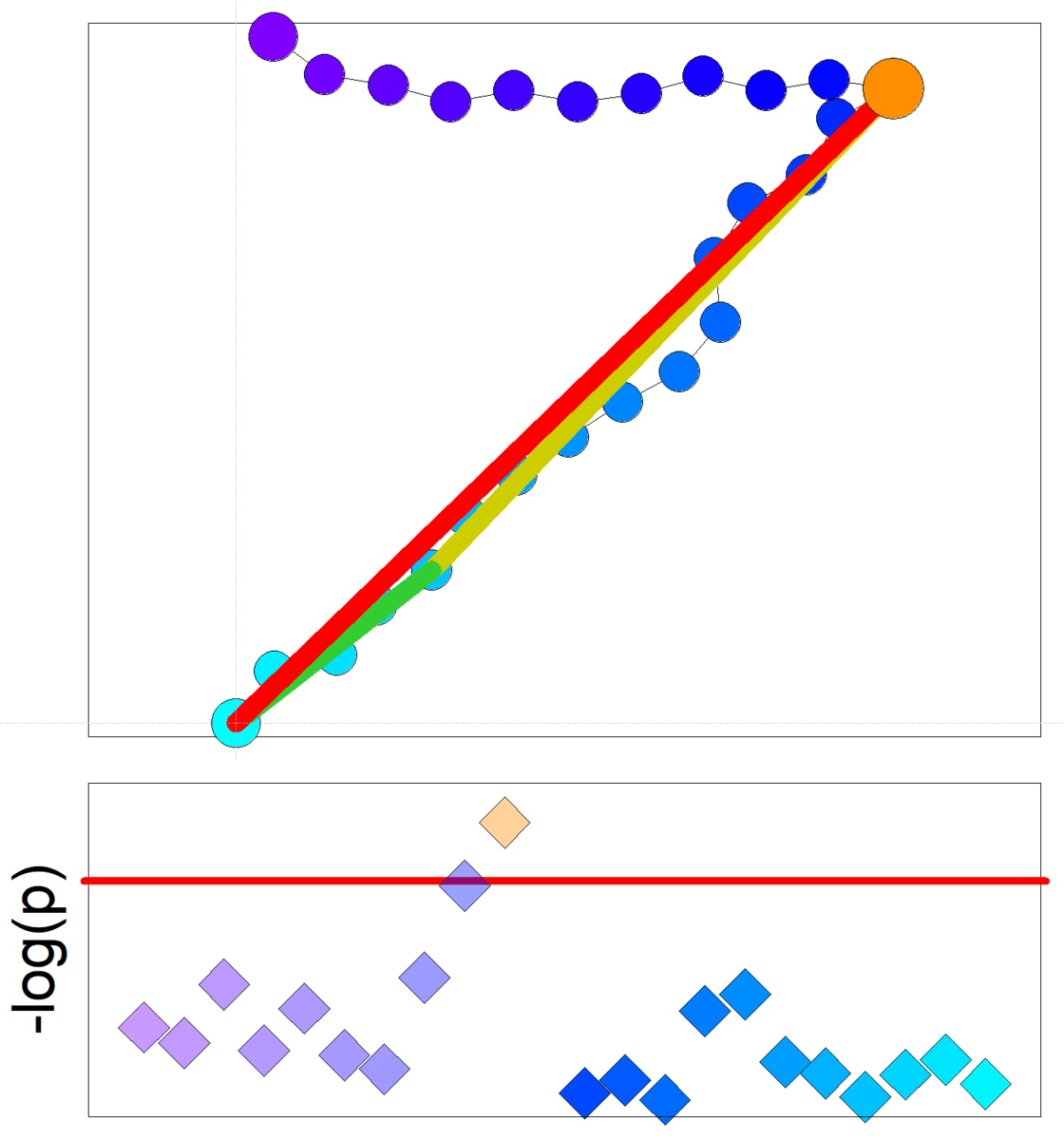
In Kooperation mit Prof. Dr. Viktor Krozer und Dr. Giacomo Ulisse, Physikalisches Institut, Arbeitsgruppe Terahertz-Photonik, Goethe-Universität Frankfurt Nichtinvasive Diabetesmessungen mit Millimeterwellen-Spektrometer Die Daten für die nichtinvasive Untersuchungen an Mäusen wurden mit Hilfe eines Millimeterwellen-Spektrometers erhalten. Das Instrument misst den Durchgang und die Reflexion von elektromagnetischen Wellen durch eine Hautfalte. Das Spektrometer arbeitet derzeit im Frequenzbereich 75 - 110 GHz.

1. Amina Felic und Sandra Pejic: Einführung in den Datensatz und Hauptkomponentenanalyse

Wir untersuchen einen hochdimensionalen Datensatz aus Amplituden- und Phasenmessungen multipler Frequenzen, die an gesunden und verschiedenen Gruppen diabetischer Mäuse erhoben wurden [1]. Durch die hohe Korrelation der gegebenen Variablen können die Daten gut in wenigen Dimensionen dargestellt werden. Dies geschieht mit Hilfe der Hauptkomponentenanalyse, die die Variablen durch Hauptachsentransformationen auf wenige Dimensionen reduziert, die möglichst viel Varianz der Originaldaten erhalten [2]. Damit lässt sich der gegebene 25-dimensionale Datensatz in zwei bis drei Dimensionen darstellen, wobei die neuen Hauptachsen über 90% der ursprünglichen Varianz abbilden und die verschiedenen Gruppen von Mäusen bereits visuell zu gewissem Grad separiert werden können. [1] Moreno-Oyervides, Aguilera-Morillo, de la Cruz Fernandez, Pascual, Jimenez, Krozer, Acedo (2021) Clinical assessment of W-band spectroscopy for non-invasive detection and monitoring of sustained hyperglycemia. Biomedical Optics Express. 12 (8), 5008-5022 [2] I. T. Jolliffe, 2002. Principal component analysis, 2nd ed., Springer New York Inc.

2. Isabella Bauer: Multivariate zwei-Stichproben Vergleiche

Lassen sich die hinsichtlich ihres Gesundheitsstatus verschiedenen Gruppen auf Basis der durchgeführten nicht-invasiven Messungen unterscheiden? Wir führen paarweise Tests durch und untersuchen so je zwei Gruppen auf statistisch signifikante Unterschiede zwischen den Gruppenmittelwerten. Zur Anwendung kommen parametrische Verfahren wie Hotellings T2-Test [3] sowie nicht-parametrische Verfahren wie Permutationstests. Im Gesamtdatensatz waren die Unterschiede zwischen allen Paaren von Mausgruppen statistisch signifikant, ebenso die Unterschiede zwischen diabetischen Patienten und gesunden Kontrollprobanden. [3] T. W. Anderson, 2003. An Introduction to Multivariate Statistical Analysis, Third Edition. John Wiley & Sons.

3. Hermann Schulz und Jan-Lukas Wermuth: Multivariate Gruppenunterschiede zwischen vielen Gruppen: MANOVA und LDA

Findet man Unterschiede in der Beeinflussung der Amplitude oder Phase von Wellen unterschiedlicher Frequenzen, wenn man sie durch die Rückenfalte von gesunden bzw. diabetischen oder adipösen Mäusen schickt? Um diese multivariaten Gruppenunterschiede statistisch zu untersuchen, verwenden wir im ersten Schritt eine multivariate Varianzanalyse (MANOVA). Wir diskutieren ihre Eigenschaften und Anwendbarkeit in Abhängigkeit von der Anzahl Beobachtungen bzw. Variablen. Unterschiede zwischen den beobachteten Gruppen waren hochsignifikant. In einem zweiten Schritt verwenden wir eine lineare Diskriminanzanalyse (LDA), bei der die mehrdimensionalen Daten sukzessive auf Achsen projiziert werden, die die Gruppen möglichst gut trennen. Die Güte der resultierenden Klassifizierungsregeln wird im Anschluss durch eine Aufteilung in Trainings- und Testdaten gemessen, und wir beobachten eine korrekte Klassifikation von über 92% bei den beobachteten Mausdaten. [4] K.V. Mardia, J.T. Kent and J.M. Bibby (1979). Multivariate Analysis. New York: Academic Press.

4. Rüdiger Krämer: Klassifikation per Support Vector Machine

Neben Modellen, die in der Statistik üblich sind, gibt es auch aus dem Bereich Machine Learning eine Vielzahl von Methoden, um Klassifizierungsprobleme zu behandeln [5]. Eine dieser Methoden ist die Support Vector Machine (SVM, [6]). Die SVM nutzt diejenigen Datenpunkte zur Trennung, die im Grenzbereich der unterschiedlichen Gruppen liegen. Diese werden als Support Vektoren bezeichnet. Obwohl die SVM auch gute Möglichkeiten zur nicht-linearen Trennung bietet, lassen sich die Ergebnisse im Vergleich zur linearen Trennung in unserem Fall damit nicht deutlich verbessern. Zur Beurteilung der Ergebnisse wurde in erster Linie Kreuzvalidierung verwendet. Bei Trennung der Daten von Mäusen lieferte die SVM gute Ergebnisse. [5] T. Hastie, R. Tibshirani, J. Friedman (2009) The Elements of Statistical Learning: Data Mining, Inference, Prediction Springer Series in Statistics. [6] C. Cortes, V. Vapnik (1995) Support-Vector Networks. Machine Leaming, 20, 273-297

Thema 2: Detektion von Richtungsänderungen in der Bewegung von Zellorganellen

Im Rahmen des LOEWE-Schwerpunkts CMMS 'Multiscale Modelling in the Life Sciences'. In Kooperation mit Prof. Dr. Enrico Schleiff und Philipp Gebhardt, Institut für molekulare Zellbiologie der Pflanzen, Goethe-Universität Frankfurt

5. Philipp Baumgärtner und Per Andres Pohlmann: Ein geometrischer Ansatz zur Analyse von Richtungsänderungen

Wir untersuchen die durch PCA auf zwei Dimensionen reduzierten Bewegungsdaten von Plastiden in Pflanzenzellen auf die Zeiten der Richtungsänderungen. Dafür bewegen wir zwei Fenster variabler Länge über den Track und betrachten zwei statistische Verfahren, um zu testen, ob der Punkt zwischen diesen Fenstern als Change Point betrachtet werden könnte: Der High Concentration F-Test kann insbesondere im Fall hoher Konzentration der Winkelverteilungen eingesetzt werden [7], im allgemeinen Fall verwenden wir ein Permutationsverfahren nach Byrne [8]. Die Teststatistik beider Tests basiert auf der Tatsache, dass die Länge der Summe zweier Vektoren kleiner oder gleich der Summe der Längen dieser Vektoren ist, wobei Gleichheit bei linearer Anhängigkeit der beiden Vektoren eintritt. [7] K.V. Mardia, P.E. Jupp, 2000. Directional statistics, J. Wiley & Sons. [8] R.W. Byrne et al., 2009. Animal Behaviour, Elvsevier Ltd

6. Annika Meyer und Michal Mazur: Hidden Markov Modelle zur Analyse von Bewegungsmustern

Das Hidden Markov Modell ist ein stochastisches Modell, welches mit Hilfe einer Markov Kette von versteckten Zuständen unterliegende Prinzipien der Organellbewegungen explorieren soll. In unserem Vortrag gehen wir davon aus, dass die Organellen zu jedem gemessenen Zeitpunkt einen Winkel und eine Schrittweite wählen, deren Verteilung vom versteckten Zustand abhängt (modifiziert nach [9]). Ziel ist es, die Anzahl und Art der Zustände so zu wählen, dass die Daten möglichst gut beschrieben werden. Anhand eines empirischen Bewegungsmusters diskutieren wir Modelle mit zwei bzw. drei Zuständen, die sich paarweise in den Verteilungen ihrer Schrittlängen und Winkel gut unterscheiden lassen und damit Rückschlüsse auf unterschiedliche Bewegungsprinzipien nahelegen. [9] Michelot, T.; Langrock, R.; Patterson, T. A. (2016): moveHMM: an R package for the statistical modelling of animal movement data using hidden Markov models. In Methods in Ecology and Evolution 7 (11), pp. 1308-1315

Semesterprogramm

Ca. 60-minütige Vorträge mit Diskussion

1. Einführung in den Datensatz und Hauptkomponentenanalyse

14. April      Amina Felic und Sandra Pejic

2. Multivariate zwei-Stichproben Vergleiche

21. April      Isabella Bauer

3. Diskriminanzanalyse und multivariate Varianzanalyse

28. April      Hermann Schulz und Jan-Lukas Wermuth

4. Klassifikation per Support Vector Machines

5. Mai      Nathan Hütsch und Rüdiger Krämer

5. Ein geometrischer Ansatz zur Analyse von Richtungsänderungen

12. Mai      Philipp Baumgärtner und Per Andres Pohlmann

6. Hidden Markov Modelle zur Analyse von Bewegungsmustern

19. Mai      Michal Mazur und Annika Meyer

Kurzpräsentationen 20-30 Min

9. Juni      Vortrag 1.+2.
23. Juni      Vortrag 3.+4.
30. Juni      Vortrag 5.+6.
7. Juli      Vortrag 7.

Abschlusspräsentation

voraussichtlich 14. Juli 2022

Allgemeine Informationen

Das Statistische Praktikum richtet sich an Studierende der Mathematik mit Statistikkenntnissen (Voraussetzung: bestandene Klausur Statistik 1, Teilnahme an der Vorbesprechung). In Kooperation mit Anwendern werden statistische Denkweisen und Methoden anhand von Daten und Fragestellungen erprobt, die aus der Praxis kommen. Das Statistische Praktikum ist ähnlich konzipiert wie ein Seminar. Themenvergabe erfolgt nach bestandener Klausur, die Bearbeitung der Themen umfasst

- die theoretische Auseinandersetzung mit einem statistischen Verfahren,
- die Anwendung des Verfahrens auf einen Datensatz,
- die intensive Auseinandersetzung mit einem komplexen Datensatz (hoher Programmieraufwand, R)
- die Präsentation von statistischer Methode und Analyseergebnissen (Folien),
- die aktive Mitarbeit im Seminar sowie ggf. Neuanalyse von Datensätzen nach Diskussion im Seminar,
- die Zusammenfassung der eigenen Hauptergebnisse in einem Kurztext (2-3 Sätze) und einer Figur.

Zum Abschluss werden die Ergebnisse in einer Abschlusspräsentation vorgestellt (10 Minuten pro Thema, Methoden und Hauptergebnisse laienverständlich zusammengefasst). Diese Abschlusspräsentation zum Statistischen Praktikum kann als separate Veranstaltung mit 2 CPs z.B. in die Module BaM-SK oder MaM-PR-2 eingebracht werden.

Teilnahmevoraussetzungen:

1. Bestandene Klausur Statistik 1
2. Teilnahme an der Vorbesprechung (!)
3. Anmeldung per Mail am 2.2. nach der Vorbesprechung.
Weitere Informationen zu Anmeldung und Organisation des Praktikums

Hauptseite Statistisches Praktikum

Impressum      Datenschutzerklärung