Prof. Dr. Gaby Schneider
unter Mitarbeit von Solveig Plomer und Insea Schlattmeier
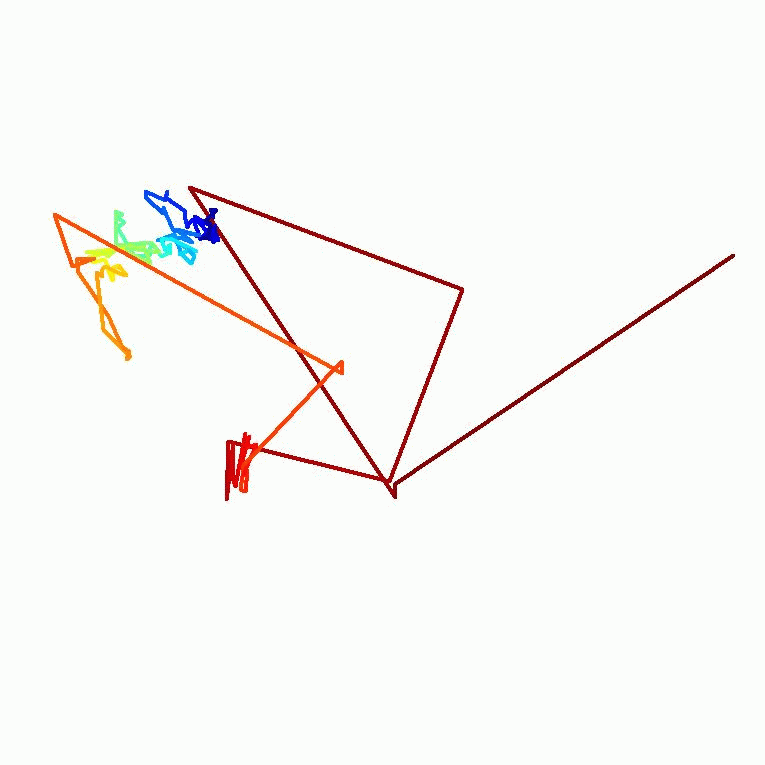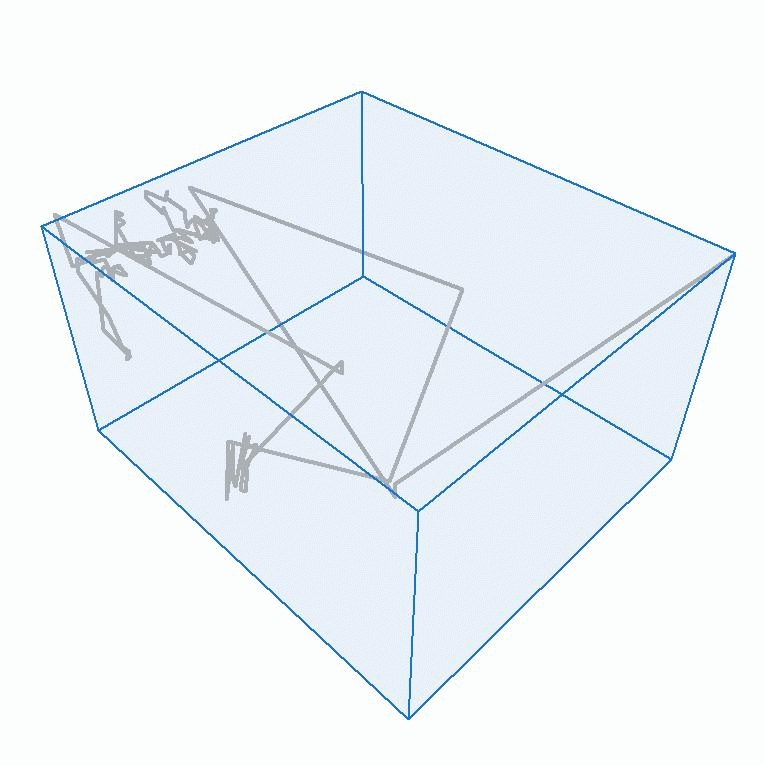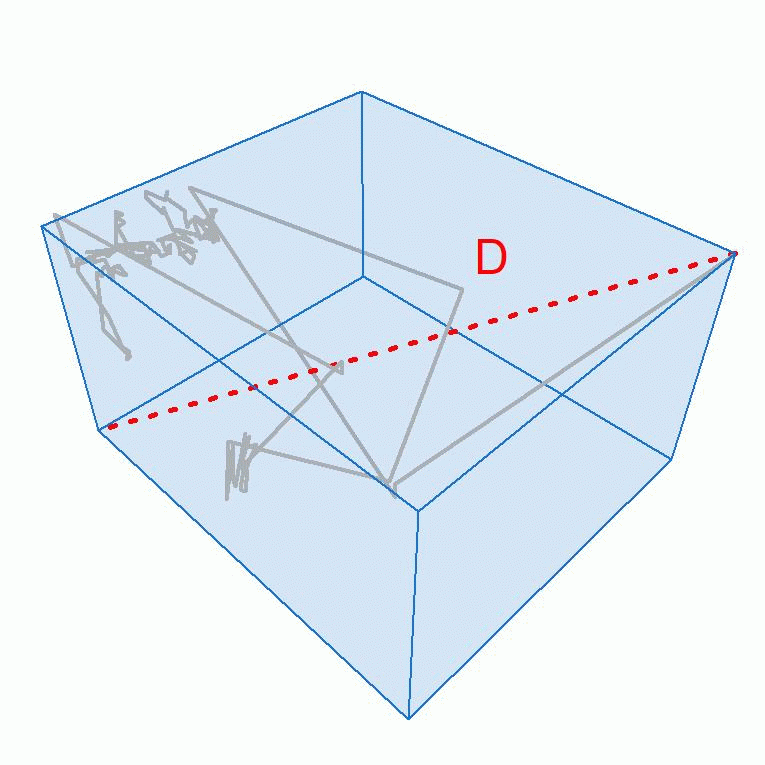
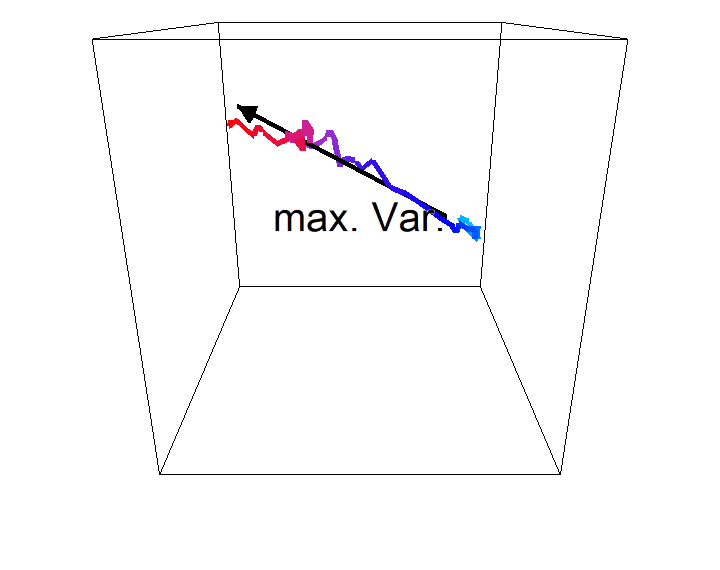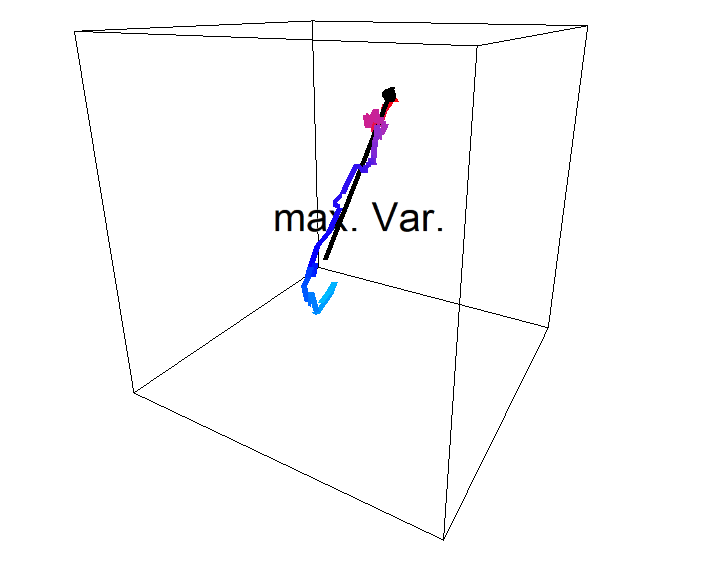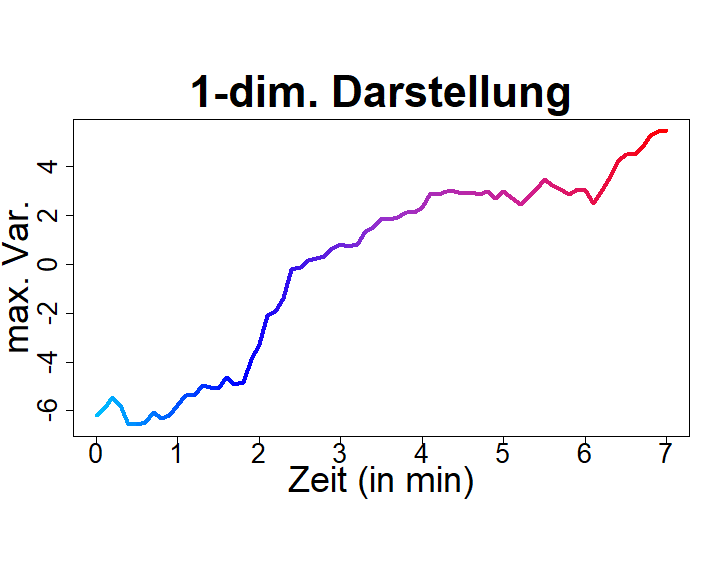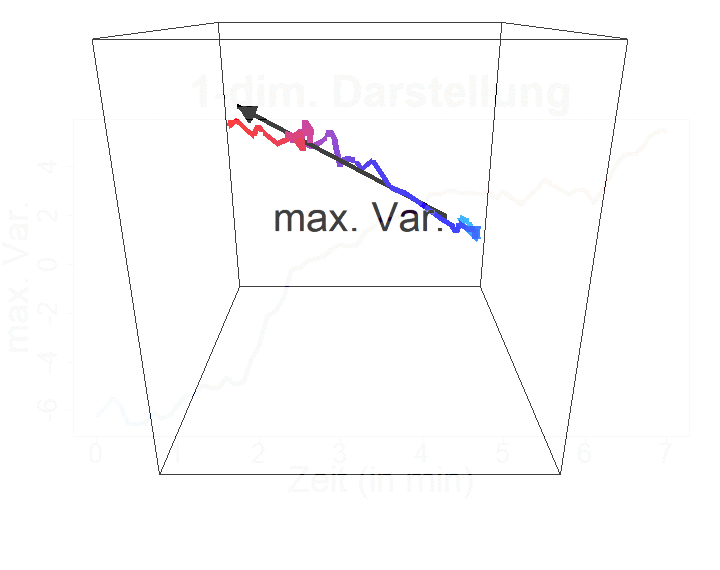
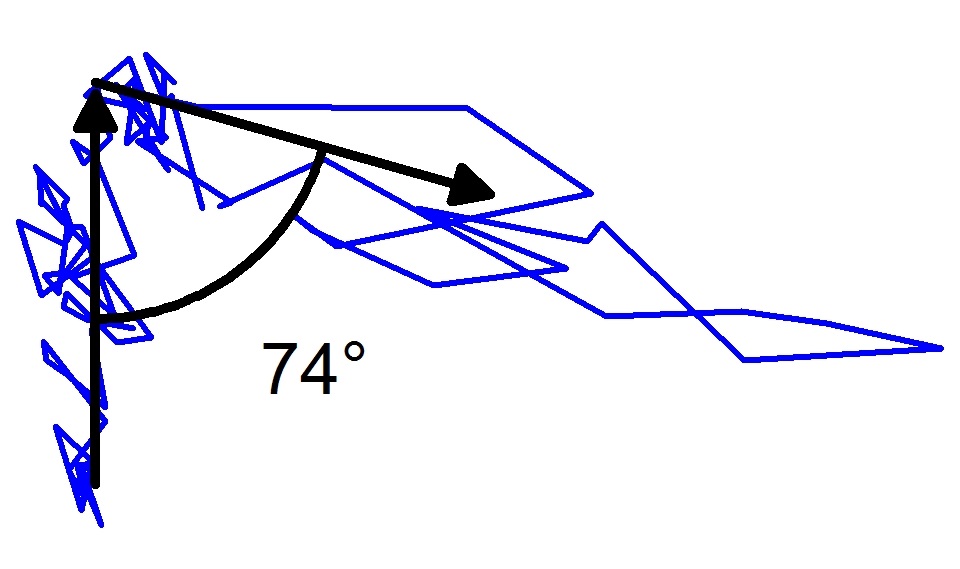
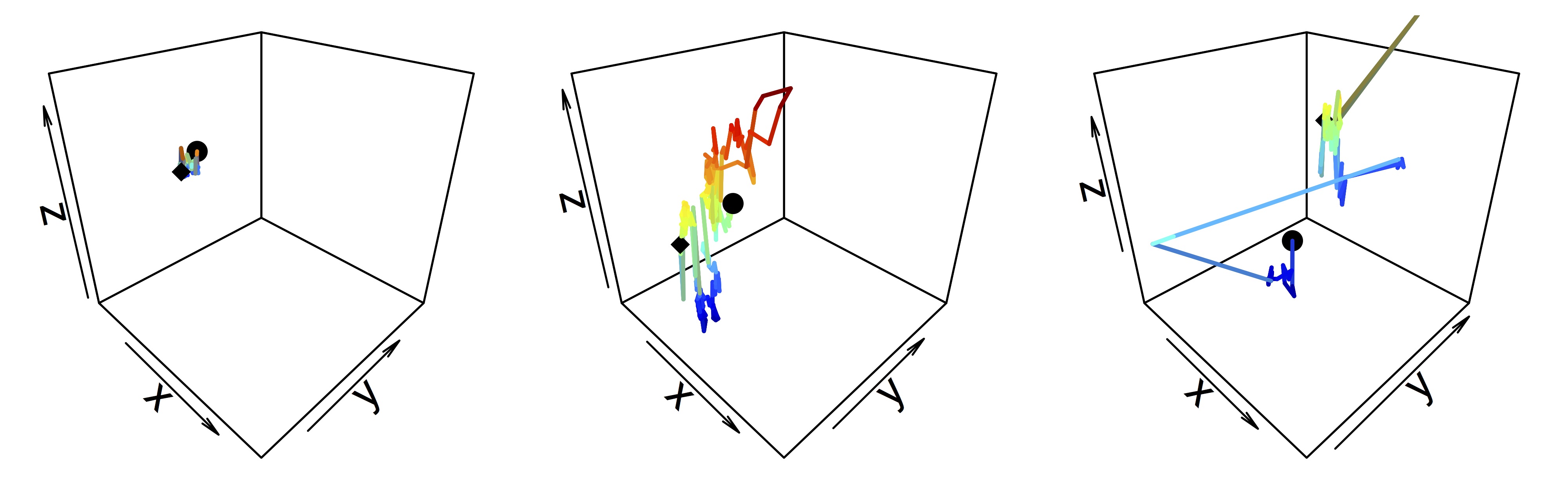
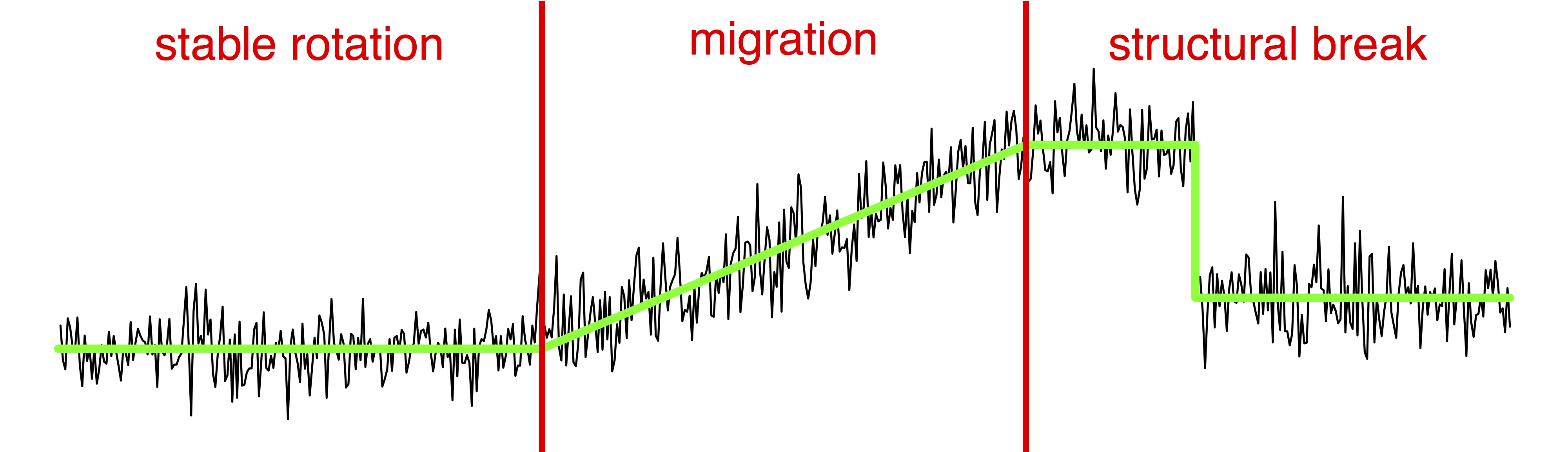
Thema 1: Stochastische Modellierung und statistische Analyse der Bewegung von ZellorganellenIn Kooperation mit Prof. Dr. Enrico Schleiff, Institut für molekulare Zellbiologie der Pflanzen, Goethe-Universität Frankfurt |
  |
|
Wir untersuchen einen Datensatz von Bewegungsmustern bestimmter Zellorganellen mit dem Ziel, diese zu klassifizieren und zu beschreiben. Die Bewegungsmuster zeigen eine hohe Variabilität von sehr kleinen, fast punktförmigen, bis hin zu schnellen, sprunghaften Bewegungen. Speziell zu den sprunghaften Bewegungen diskutieren wir potentielle Probleme bei der Datenerhebung sowie experimentelle und analytische Lösungsansätze. So sinkt etwa die Beobachtungsdauer mit steigender Geschwindigkeit der Organelle, und große Sprünge treten gehäuft an den Rändern des beobachteten Zeitfensters auf. |
|
Wir untersuchen, wie gut die Bewegungen der Organellen in weniger als drei Dimensionen dargestellt werden können. Hierfür nutzen wir die Hauptkomponentenanalyse, welche sukzessive die zueinander orthogonalen Richtungen maximaler Varianz findet. Anhand dieser Richtungen können die Bewegungen in neuen Koordinatensystemen dargestellt werden. Besteht in einer der neuen Richtungen nur wenig Variabilität, so wird durch Weglassen dieser Richtung eine Darstellung in nur ein oder zwei Dimensionen möglich, die dennoch einen Großteil der Varianz abbildet. Bei einer Reduktion auf nur eine Dimension etwa bewegt sich die Organelle annähernd entlang einer Geraden. Wir untersuchen Unterschiede in der Reduzierbarkeit der Organellbewegungen zwischen verschiedenen Mutanten und Aufnahmeframes. |
|
In den auf zwei Dimensionen projizierten Bewegungsdaten der Organellen lassen sich Bewegungen finden, die sich anscheinend entlang von Geraden bewegen und plötzlich ihre Richtung ändern. Wir wollen mithilfe einer zeitaufgelösten Hauptkomponentenanalyse den Zeitpunkt dieser Richtungswechsel detektieren. Diese schätzt die Bewegungsrichtung in zwei Fenstern der Größe h vor bzw. nach jedem Zeitpunkt und betrachtet den Prozess der Winkel zwischen diesen Richtungen. Der maximale Winkel dient als Teststatistik des Tests der Nullhypothese der Abwesenheit von Richtungswechseln. Seine Verteilung unter der Nullhypothese wird durch Simulation gewonnen. Dazu entwickeln wir stochastische Modelle, die die mit Messfehlern behaftete stückweise lineare Bewegung beschreiben. |
|
Wir untersuchen ein Verfahren zur Detektion von Changepoints, an denen sich der
Erwartungswert einer Zeitreihe ändert [1]. Dabei wird ein Maß für die Schwankung des Erwartungswertes
entwickelt und geschätzt durch die reskalierte Differenz der Mittelwerte. Einen Schätzer
für einen Changepoint liefert der Zeitpunkt, an dem diese Differenz D eine vorher
festgelegte Schwelle S überschreitet. Wir erläutern Eigenschaften des
Verfahrens anhand von Simulationen und diskutieren seine Anwendbarkeit auf die empirischen Daten der Organellbewegungen.
[1] M. Vogt, H. Dette (2015) Detecting gradual changes in locally stationary processes. The Annals of Statistics 43(2): 713-40. |
|
Ein Verfahren zur Detektion von Gipfeln in Zeitreihen wird vorgestellt [2]. Für jeden Zeitpunkt t
schätzen wir mithilfe des normalen linearen Modells die Steigung in einem Ausschnitt
vor und nach t und berechnen deren reskalierte Differenz.
Peaks sollen durch ihre charakteristische Zu- und Abnahme der Steigung zu großen Differenzen führen und so detektiert werden.
Zum Test der Nullhypothese der Abwesenheit von Peaks wird als Teststatistik
das Maximum dieser Differenzen betrachtet. Unter der Modellannahme unabhängig identisch verteilter
Messfehler kann durch Permutation ein Schwellenwert zur Ablehnung der Nullhypothese gewonnen werden.
Auch die Kombination verschiedener Ausschnittsgrößen ist möglich, um verschieden
große Gipfel besser detektieren zu können.
Wir stellen Theorie und Verfahren vor, diskutieren Eigenschaften,
Vor- und Nachteile und demonstrieren diese sowohl an idealisierten,
simulierten Daten, als auch an echten Messwerten von Neuronenaktivitäten von Mäusen in unterschiedlichen
Sedierungszuständen.
[2] M. Messer, H. Backhaus, T. Fu, A. Stroh, G. Schneider (eingereicht) A multi scale approach for testing and detecting peaks in time series |
6. Lukas Deppe und Torsten Walther - Segmented linear RegressionExistieren in einer Zeitreihe Phasen konstant niedriger neuronaler Aktivität, und unterscheidet sich ihre Länge zwischen verschiedenen experimentellen Bedingungen? Zur Beantwortung dieser Fragen unterteilen wir die Zeitreihe zunächst in sinnvolle Abschnitte und wenden dann auf diese Abschnitte eine stückweise lineare Regression an. Mit ihrer Hilfe lassen sich stückweise lineare Trends identifizieren und beschreiben. Die Zeitpunkte einer Änderung des Trends werden aus dem Modell mit den kleinsten Residuenquadraten geschätzt. Zum Vergleich verschiedener Modelle diskutieren wir varianzanalytische Verfahren und Likelihood-Quotienten-Tests [3,4]. Die Längen der Phasen konstant niedriger Aktivität verschiedener experimenteller Bedingungen werden mit einem Wilcoxon-Rangsummen-Test verglichen.[3] P. I. Feder (1975) The Log Likelihood Ratio in Segmented Regression. The Annals of Statistics 3(1): 84-97. [4] S. S. Wilks (1938) The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses. The Annals of Mathematical Statistics 9(1): 60-62. |
|
Hauptseite Statistisches Praktikum