Statistisches Praktikum im SS 2017

Prof. Dr. Gaby Schneider
unter Mitarbeit von Dr. Michael Messer, Stefan Albert, Matthias Gärtner, Solveig Plomer und Benjamin Straub

Seminar im SS 2017. Do. 12:15 Uhr, SR 711 (groß), RM 10
Vorbesprechung: Do, 9. Februar, 11:30 Uhr, Raum 110.
Abschlusspräsentation: Donnerstag, 6. Juli 2017, 12-14 Uhr, 711 (groß), RM 10
Die folgenden Abstracts wurden in Kooperation mit den Teilnehmerinnen und Teilnehmern des Statistischen Praktikums erstellt.

Thema 1: Fliegenlarven und Körperregionen

In Kooperation mit
PD Dr. Jens Amendt, Victoria Bernhardt, Institut für Rechtsmedizin, Abteilung Forensische Biologie

1. Ein Datenüberblick

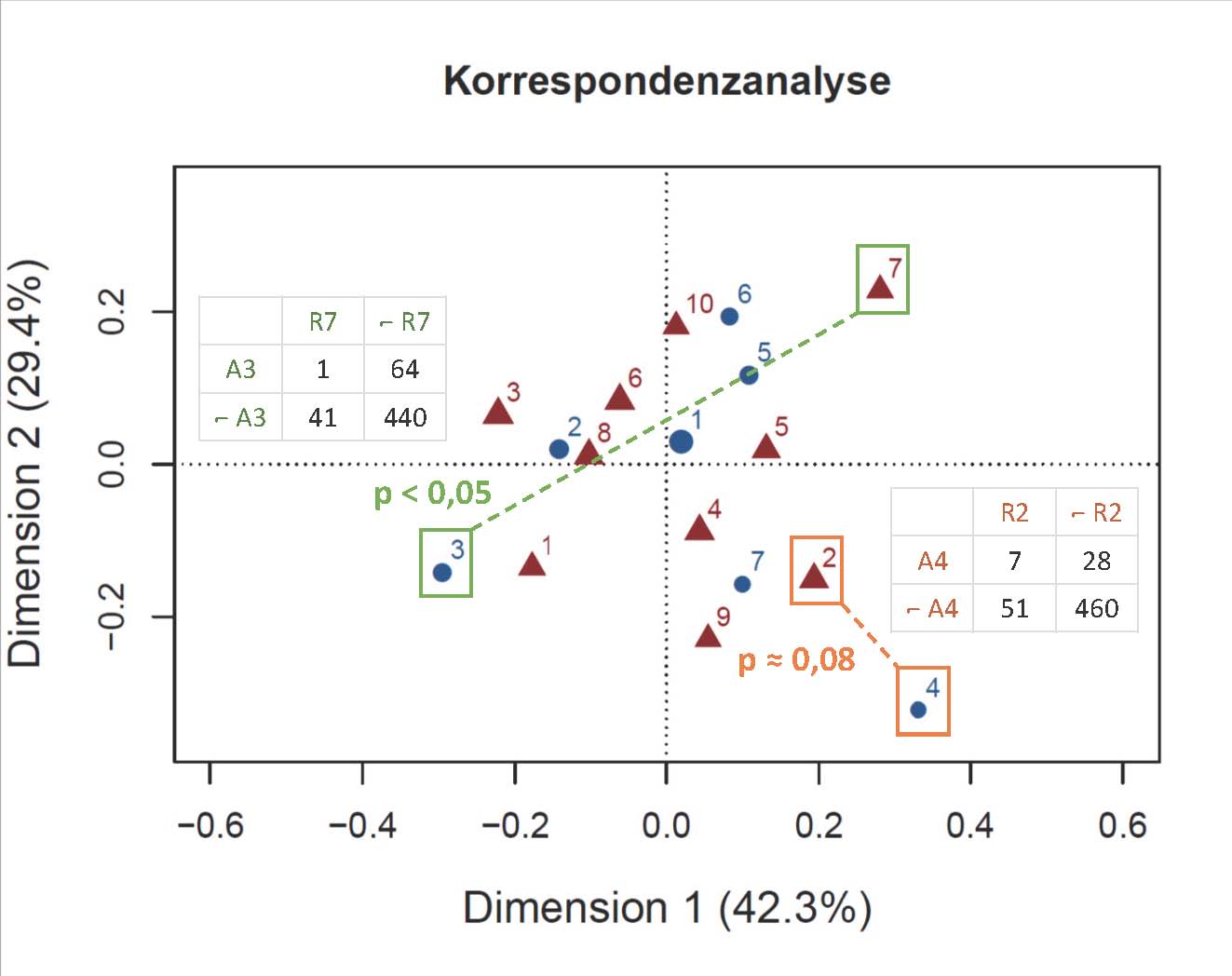
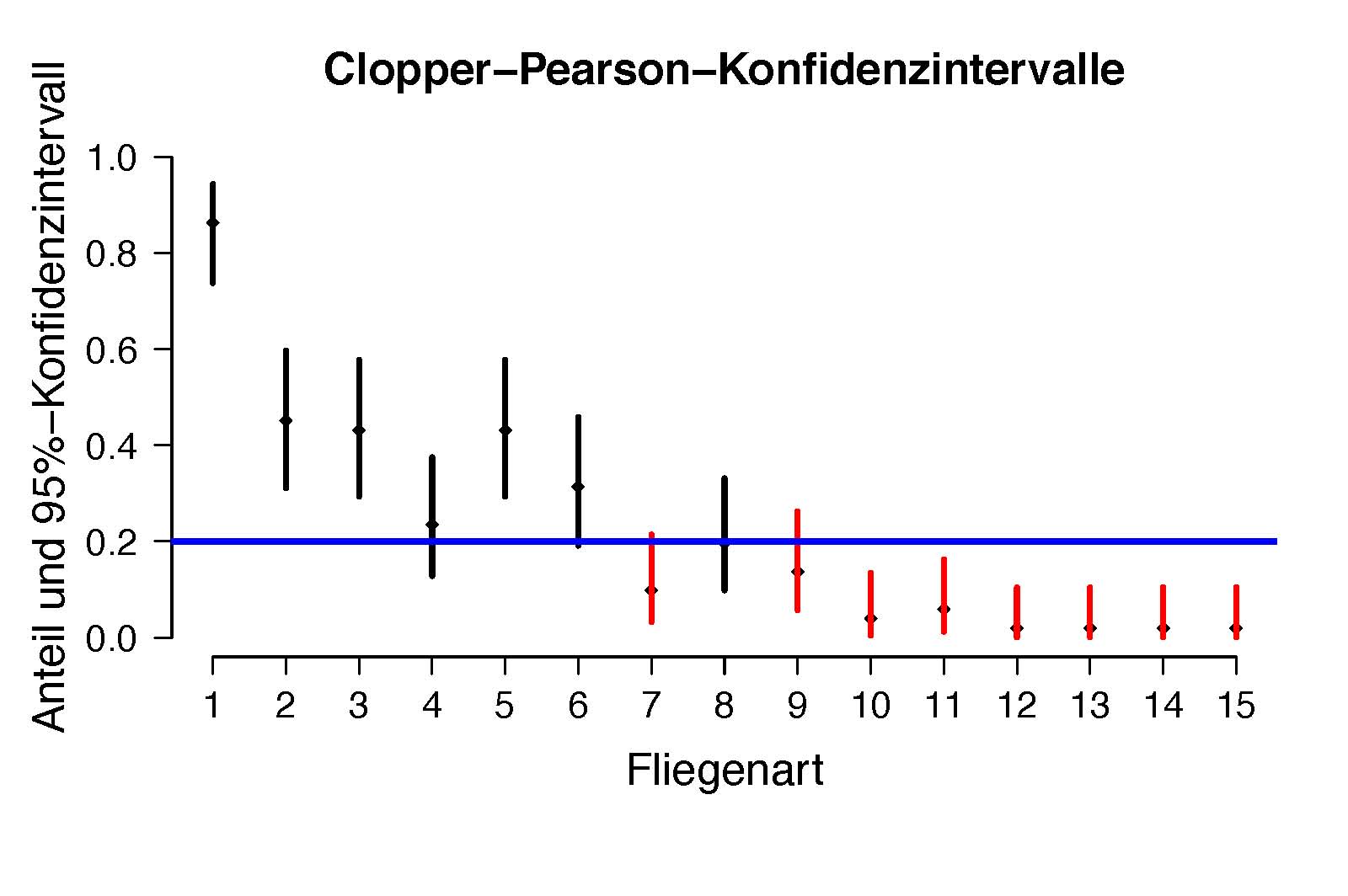
In der forensischen Biologie wurde das Auftreten bestimmter Fliegenlarven-Arten in verschiedenen Körperregionen von Leichen untersucht. Mittels deskriptiver Statistik verschaffen wir uns einen Überblick über die Verteilung der Arten auf die Regionen. Manche Arten bzw. Regionen treten nur selten auf, so dass die mittels Normalapproximation ermittelten Konfidenzintervalle keine ausreichenden Überdeckungswahrscheinlichkeiten besitzen. Stattdessen verwenden wir hier exakte Clopper-Pearson-Konfidenzintervalle. Für Fliegenarten mit einem Anteil von mindestens 20% untersuchen wir potentielle Korrelationen im Auftreten der Arten sowie deren Modulation durch temperaturabhängig bestimmte Auftretenshäufigkeiten.

[1] Clopper, Pearson (1934) Biometrika 26, 404-413

2. Korrespondenzanalyse

Mit der Korrespondenzanalyse lassen sich die Verteilungen verschiedener Arten von Fliegenlarven (Zeilen) bzw. verschiedener Körperregionen (Spalten) durch Darstellung in einem 2-dimensionalen Koordinatensystem vergleichen. Jede Zeile bzw. Spalte der Tabelle wird als ein roter bzw. blauer Punkt dargestellt. Die Abstände zwischen Punkten derselben Farbe entsprechen dem Chiquadratabstand der zugehörigen Verteilungsprofile. Zwischen Punkten verschiedener Farben zeigt die relative Lage der Punkte, wie dominant die jeweilige Zeile im Spaltenprofil bzw. die jeweilige Spalte im Zeilenprofil ist. Die Achsenbeschriftungen zeigen den Anteil des Chiquadratabstandes der Rohdaten, der in den gegebenen Dimensionen repräsentiert wird. Mit der Korrespondenzanalyse lassen sich damit graphisch Hypothesen generieren. Hier scheint z.B. Art 3 unterrepräsentiert in Region 12 und Art 4 überproportional häufig in Region 2 aufzutreten.

[2] Greenacre (1984): Theory and applications of correspondence analysis.

Thema 2: Punktprozessmodelle in der Neurophysiologie

Im Rahmen des DFG-Schwerpunkts SPP-1665 'Resolving and manipulating neuronal networks in the mammalian brain - from correlative to causal analysis'. In Kooperation mit Prof. Dr. Jochen Roeper, Dr. Sevil Duvarci, Dr. Torfi Sigurdsson, Institut für Neurophysiologie, Goethe-Universität Frankfurt

3. Korrelierte homogene Erneuerungsprozesse

Wir diskutieren ein Verfahren zur Simulation korrelierter paralleler Spiketrains und zur Schätzung der Korrelationsstruktur in empirischen Daten. Für die Simulation werden in korrelierten Poissonprozessen, die durch Überlagerung erzeugt werden, auftretende Spikes mit Hilfe von Hazard-Funktionen so ausgedünnt, dass die verbleibenden Inter-Spike-Intervalle (ISIs) vorgegebenen Zielverteilungen (z.B. Gamma-Verteilungen) folgen und eine vorgegebene Korrelationsstruktur besitzen. Durch das Abzählen von in den parallelen Spiketrains (fast) gleichzeitig auftretenden Spikes kann durch Empirical de-Poissonization die Korrelationsstruktur der parallelen Spiketrains geschätzt werden. Wir untersuchen die Simulations- und Schätzverfahren in Simulationen und studieren ihr Verhalten bei der Anwendung auf echte Spiketrains.

[3] Reimer, Staude, Ehm, Rotter (2012): Modeling and analyzing higher-order correlations in non-Poissonian spike trains. Journal of Neuroscience Methods. 208: 18-33.

4. Theresa Kumpitsch - Inhomogene Erneuerungsprozesse und Time Rescaling

Um die Kodierung neuronaler Information zu verstehen, möchten wir neuronale Feueraktivität statistisch möglichst genau beschreiben. Diese Beschreibung geschieht oft durch Erneuerungsprozesse, d.h. Punktprozesse mit unabhängig und identisch verteilten Interspike-Intervallen (ISIs). Häufig verwendete Prozesse sind neben dem Poisson-Prozess der Gamma- sowie der Invers-Gauss-Prozess. Inhomogen nennen wir Erneuerungsprozesse, wenn ihre Intensität von der Zeit abhängt. Ogatas Thinning sowie das Times-Rescaling-Theorem (und daran angelehnte Transformationen) bieten eine Möglichkeit, solche Prozesse zu simulieren. Umgekehrt kann man mit Hilfe des Time-Rescalings auch die Güte von Modellannahmen an einen gegebenen Spiketrain testen.

[4] Barbieri, Quirk, Frank, Wilson, Brown (2001) Journal of Neuroscience Methods 105: 25-37.
[5] Brown, Barbieri, Ventura, Kass, Frank (2001) Neural Computation 14: 325-46.

5. Insea Schlattmeier - Conditional Intensity, Hawkes Prozesse

Hawkes Prozesse sind Punktprozesse, die über eine Conditional Intensity definiert sind, d.h. die Intensität zum Zeitpunkt t hängt ab von der Vergangenheit des Prozesses bis zum Zeitpunkt t.

Wir betrachten einen Spezialfall: Nach jedem Ereignis steigt die Conditional Intensity zunächst an und fällt danach wieder ab. Simulationsmethoden verwenden Ogata's Thinning, Time Rescaling und eine Darstellung über Galton Watson Prozesse. Bei letzterer werden Mutterpunkte mit Hilfe eines homogenen Poissonprozesses generiert, wobei jeder Punkt seinerseits eine Poissonverteilte Anzahl Nachkommen mit gegebener Intensitätsfunktion hervorbringt. Mit Hilfe von Hawkes Prozessen lässt sich eine Vielzahl von Mustern darstellen. Wir untersuchen die Güte der Parameterschätzung per Maximum Likelihood und studieren, ob der Hawkes Prozess eine geeignete Methode darstellt zur Beschreibung eines Datensatzes von an wachen Mäusen gewonnenen Spiketrains dopaminerger Neurone.

[6] Rasmussen (2011) Temporal point processes: the conditional intensity function.
[7] Laub, Taimre, Pollett (2015) Hawkes Processes, arXiv:1507.02822

Allgemeine Informationen

Das Statistische Praktikum richtet sich an Studierende der Mathematik mit Statistikkenntnissen (Voraussetzung: bestandene Klausur Statistik 1). In enger Kooperation mit Anwendern werden statistische Denkweisen und Methoden anhand von Daten und Fragestellungen erprobt, die aus der Praxis kommen. Das Statistische Praktikum ist ähnlich konzipiert wie ein Seminar. Themenvergabe erfolgt nach bestandener Klausur, die Bearbeitung der Themen umfasst

- die theoretische Auseinandersetzung mit einem statistischen Verfahren,
- die Anwendung des Verfahrens auf einen Datensatz,
- die intensive Auseinandersetzung mit einem komplexen Datensatz (hoher Programmieraufwand, R)
- die Präsentation von statistischer Methode und Analyseergebnissen (Folien),
- die aktive Mitarbeit im Seminar sowie ggf. Neuanalyse von Datensätzen nach Diskussion im Seminar,
- die Zusammenfassung der eigenen Hauptergebnisse in einem Kurztext (2-3 Sätze) und einer Figur.

Zum Abschluss werden die Ergebnisse in einer Abschlusspräsentation vorgestellt (10 Minuten pro Thema, Methoden und Hauptergebnisse laienverständlich zusammengefasst). Diese Abschlusspräsentation zum Statistischen Praktikum kann als separate Veranstaltung mit 2 CPs z.B. in die Module BaM-SK oder MaM-PR-2 eingebracht werden.

Hauptseite Statistisches Praktikum