Statistisches Praktikum im SS 2015
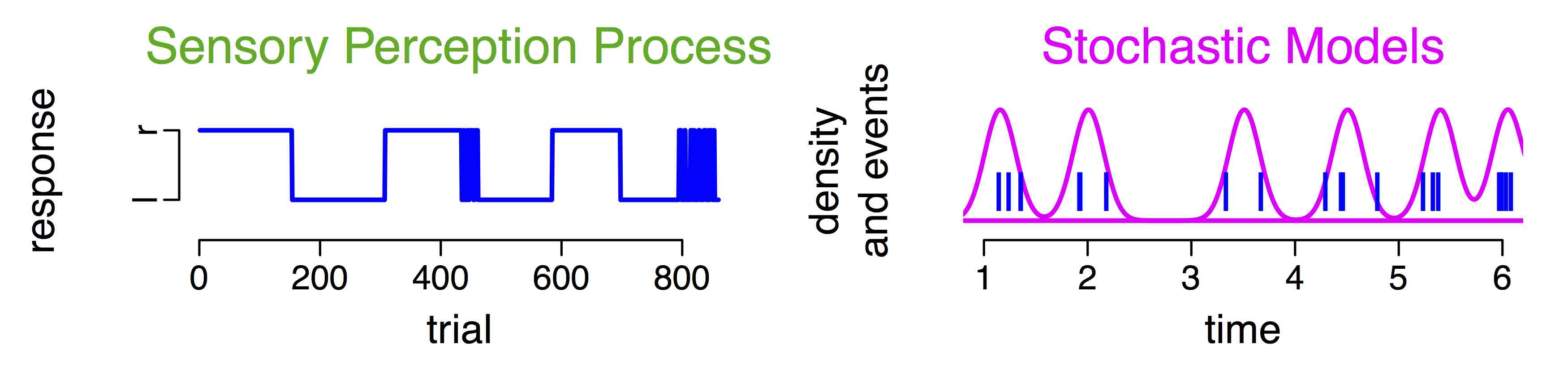
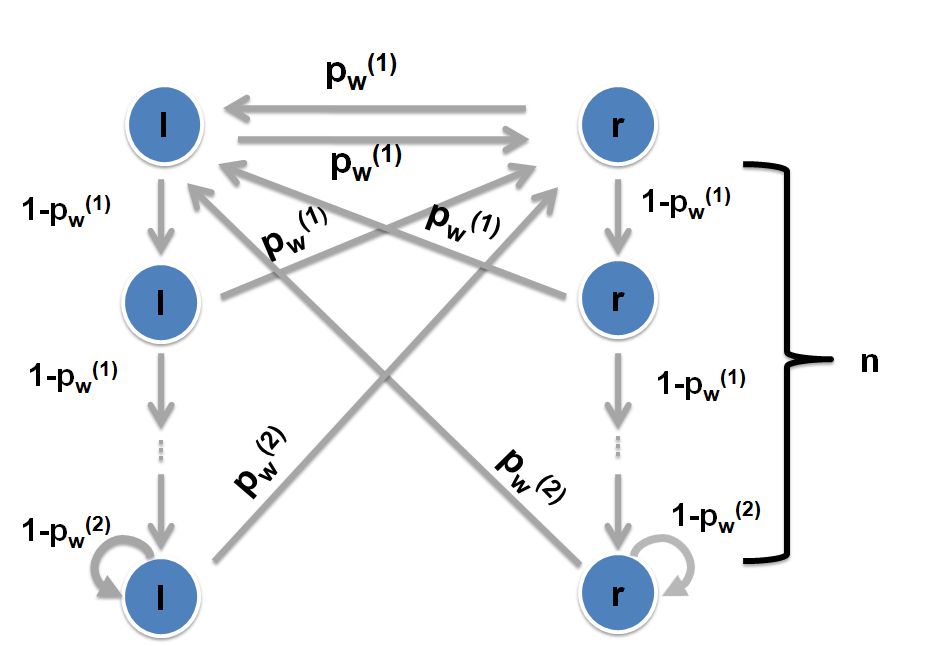
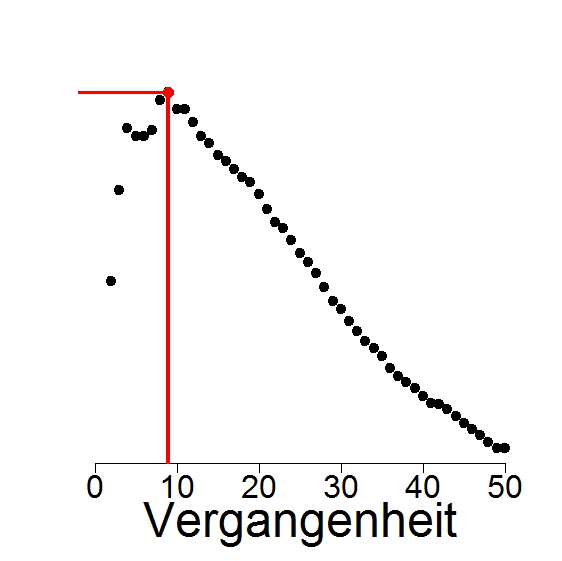
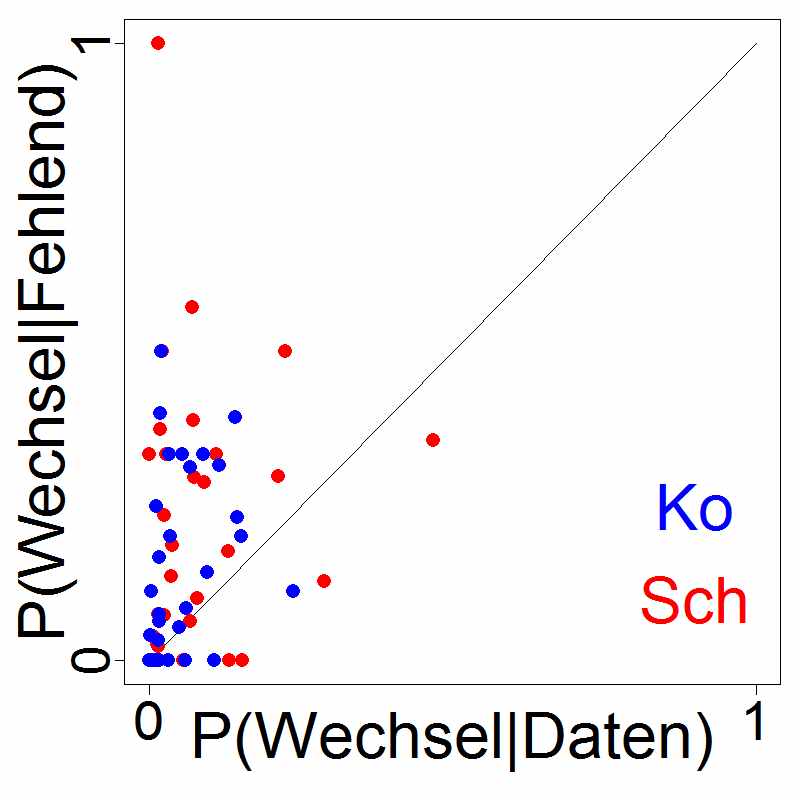
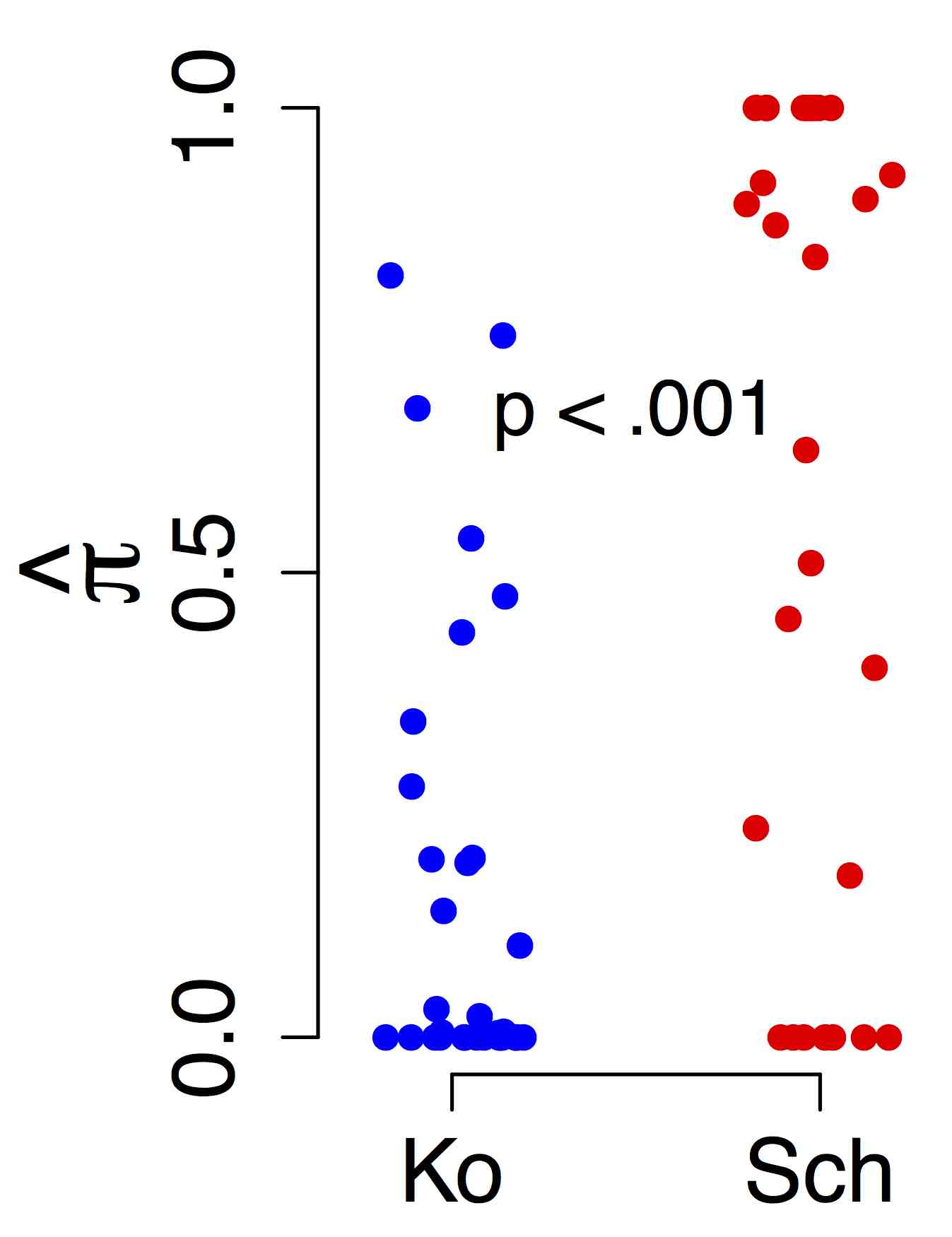
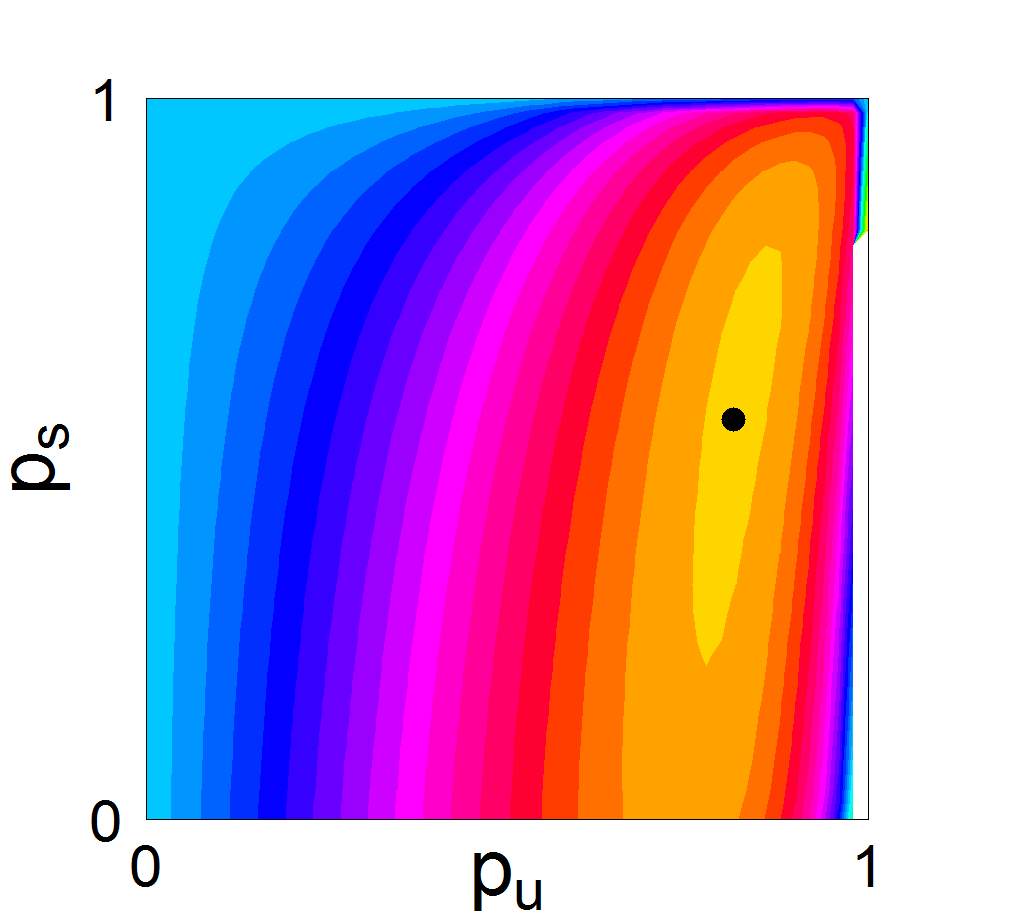
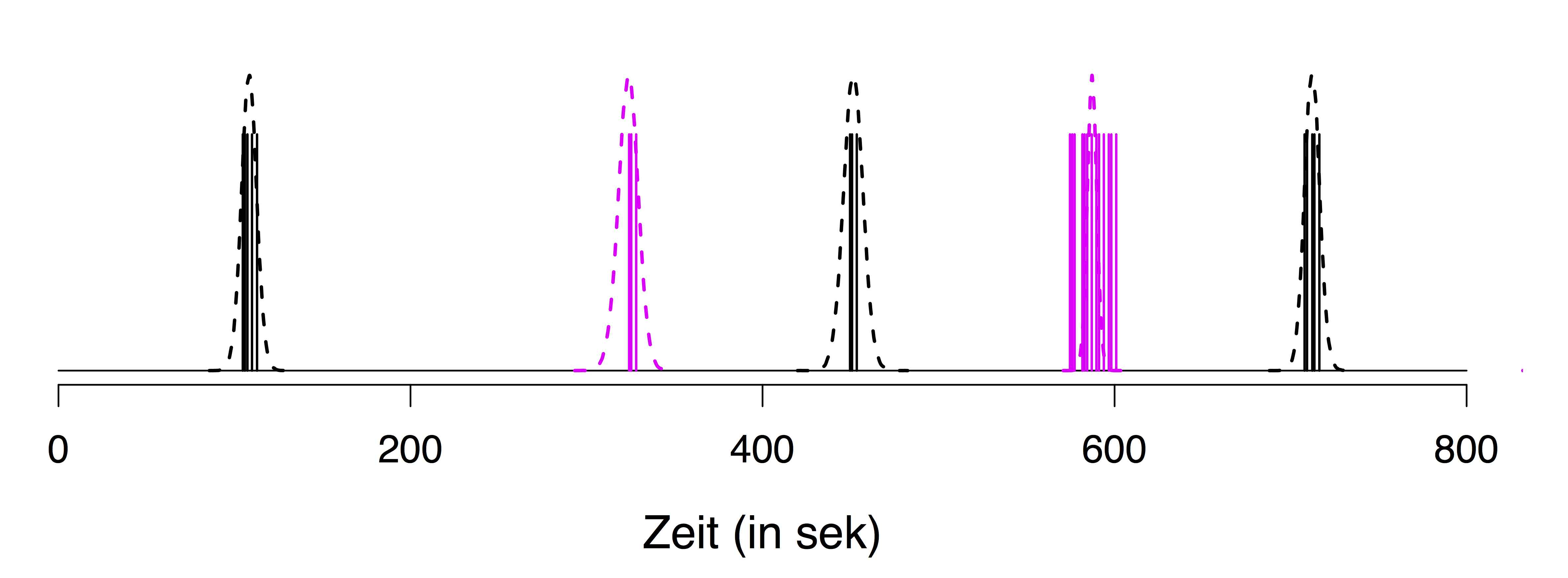
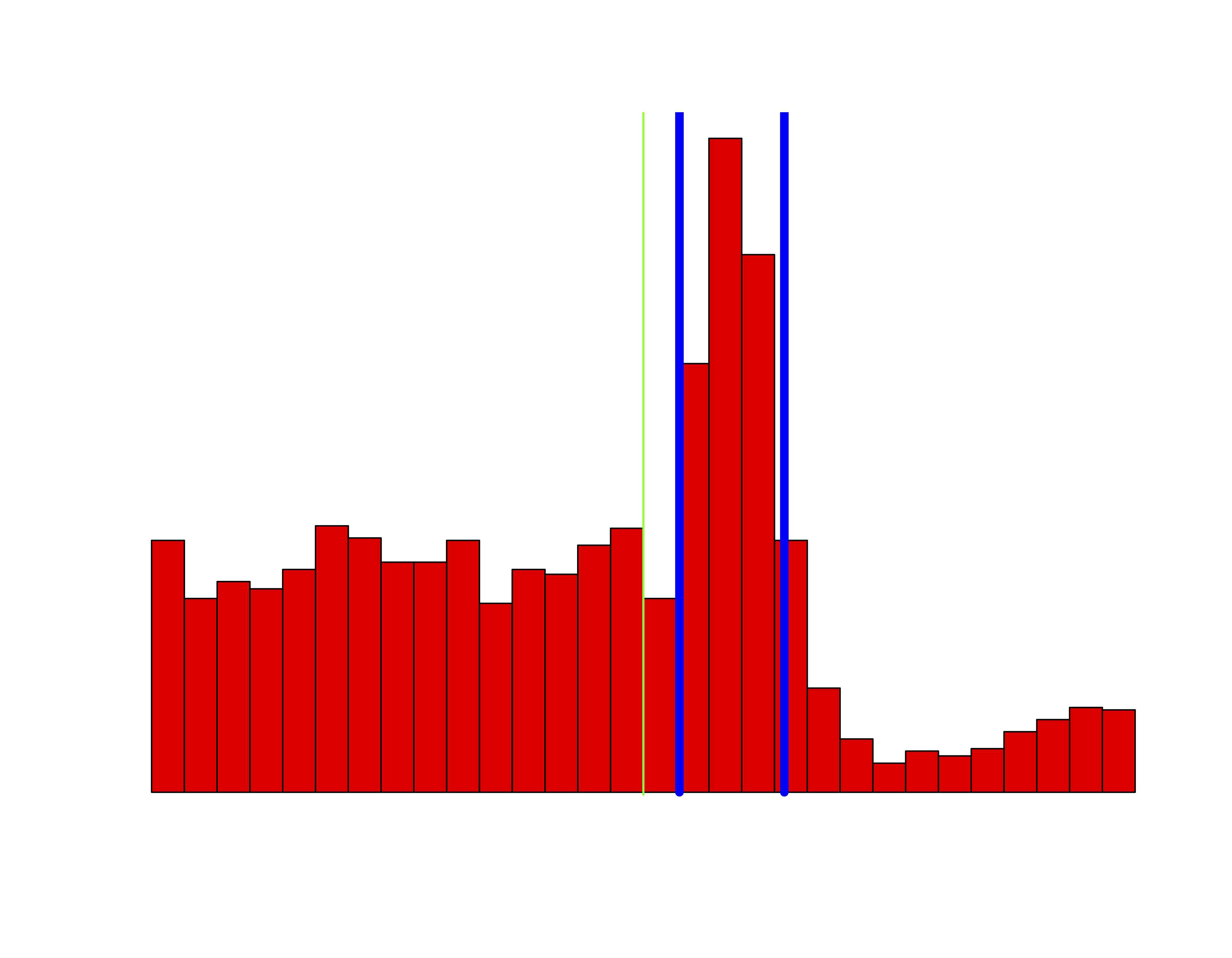
Stochastische Modelle für bistabile Wahrnehmung
Apl. Prof. Dr. Gaby Schneider
unter Mitarbeit von Stefan Albert, Matthias Gärtner und Benjamin Straub

|
Im Rahmen des vom BMBF geförderten Verbundprojekts PsychoSys - Die Rolle von Dopamin bei perzeptueller Inferenz und Wahn der e:MED Systems Medicine Juniorverbünde. In Kooperation mit Dr. Katharina Schmack, Charite Berlin, Dr. Simon Jacob, TU München, Dr. Torfi Sigurdsson, Institut für Neurophysiologie der Goethe-Universität Frankfurt |