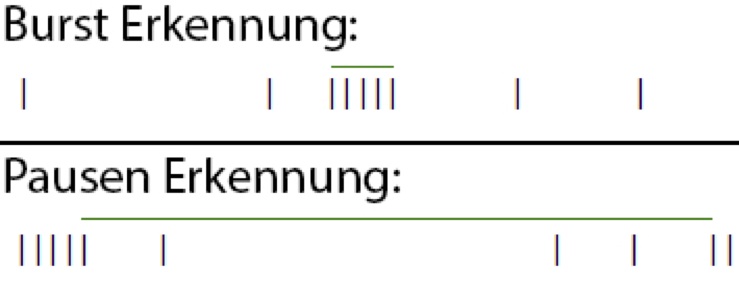
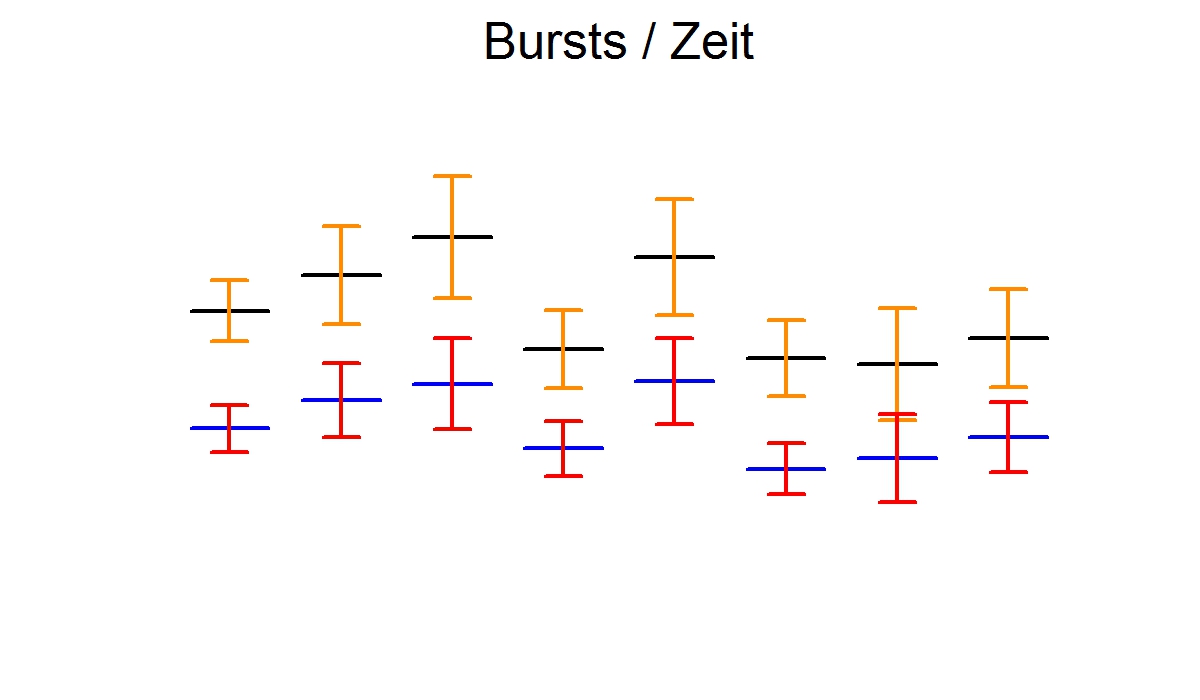
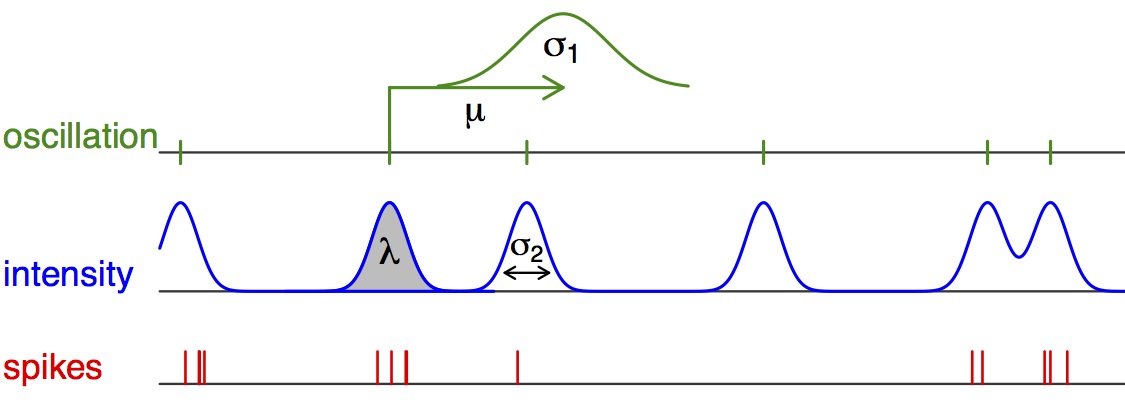
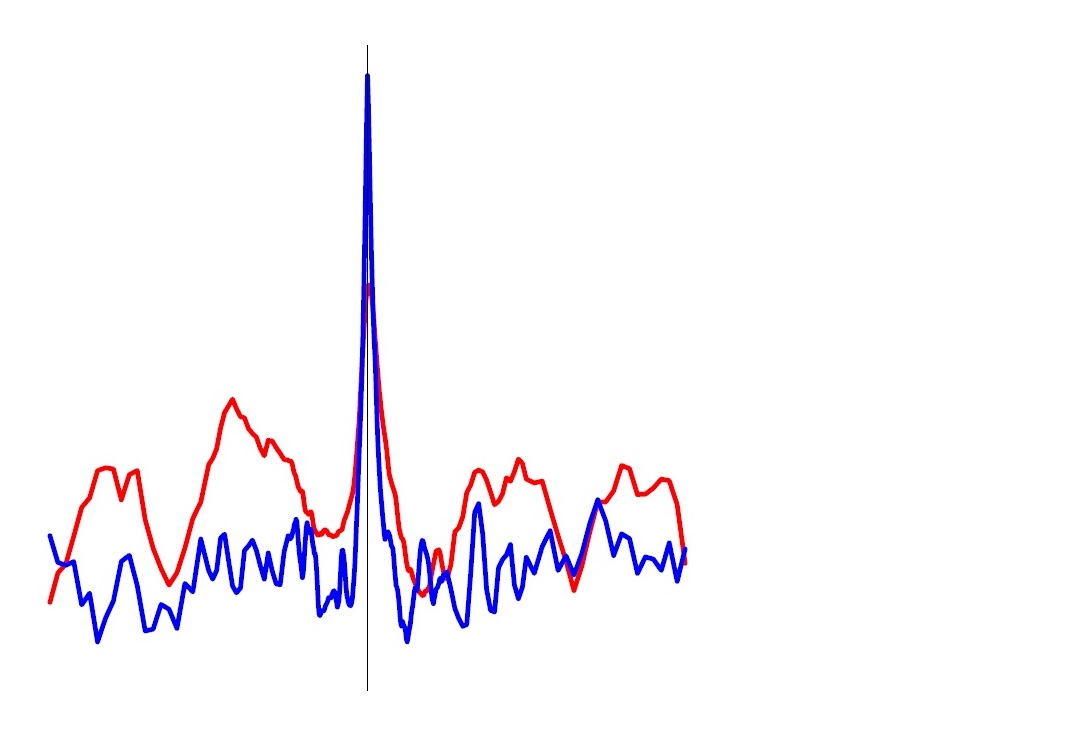
Statistisches Praktikum im SS 2014
Prof. Dr. Gaby Schneider
unter Mitarbeit von Benjamin Straub, Matthias Gärtner und Dr. Michael Messer
Im Rahmen des DFG-Schwerpunkts SPP-1665 'Resolving and manipulating neuronal networks in the mammalian brain - from correlative to causal analysis'
in Kooperation mit Prof. Dr. Jochen Roeper, Dr. Sevil Duvarci, Dr. Torfi Sigurdsson, Institut für Neurophysiologie, Goethe-Universität Frankfurt| Wann: Wo: Beginn: |
Di. 12:15 Uhr Seminarraum 711 (klein), Robert-Mayer-Str. 10 22.4.2013 |